
【题目】已知抛物线![]() :
:![]() (m>0)的顶点为M,交y轴于点G.
(m>0)的顶点为M,交y轴于点G.
(1)如图,若点G坐标为(0,![]() )
)
①直接写出抛物线![]() 解析式;
解析式;
②点Q在y轴上,将线段QM绕点Q逆时针旋转90°得线段QN,若点N恰好落在抛物线![]() 上,求点Q的坐标.
上,求点Q的坐标.
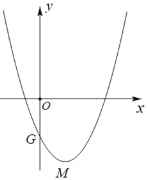
(2) 探究: 将抛物线![]() 沿唯一的定直线x=a对称得抛物线
沿唯一的定直线x=a对称得抛物线![]() ,记抛物线
,记抛物线![]() 交y轴于点P (0,-2m),求a的值.
交y轴于点P (0,-2m),求a的值.
【答案】(1)①![]() ;②Q1(0,
;②Q1(0,![]() ),Q2(0,-
),Q2(0,-![]() );(2)1
);(2)1
【解析】
(1)①将点G的坐标代入到二次函数解析式中即可求出结论;
②设点Q(0,t),过点N作NA⊥y轴于点A,过点M作NB⊥y轴于点B,利用AAS证出△ANQ≌△BQM,求出二次函数图象的顶点坐标即可求出点N的坐标,然后将点N的坐标代入解析式中即可求出t的值,从而求出点Q的坐标;
(2)将二次函数的一般式转化为顶点式即可求出点M的坐标,然后求出抛物线![]() 的顶点坐标,将点P的坐标代入得出关于a的一元二次方程,利用a有唯一值令△=0即可求出m的值,从而求出a的值.
的顶点坐标,将点P的坐标代入得出关于a的一元二次方程,利用a有唯一值令△=0即可求出m的值,从而求出a的值.
解:(1)①将点G(0,![]() )代入解析式中,得
)代入解析式中,得
![]()
解得:m=1或-1(不符合条件,舍去)
将m=1代入解析式中,得
![]() ;
;
②设点Q(0,t),过点N作NA⊥y轴于点A,过点M作NB⊥y轴于点B,
∴∠NAQ=∠MBQ=90°,
又QM=QN,∠MQN=90°,
∴∠ANQ+∠AQN=90°,∠BQM+∠AQN=90°
∴∠ANQ=∠BQM
∴△ANQ≌△BQM,
∴AN=BQ,AQ=BM,
由点M 得M(1,
得M(1,![]() ),即B(0,
),即B(0,![]() ),
),
∴BM=AQ=1,BQ=AN=t+![]() ,
,
∴A(0,t+1),即N(t+![]() ,t+1),
,t+1),
则有(t+![]() )2-2(t+
)2-2(t+![]() )-
)-![]() =t+1,
=t+1,
解得t1=![]() ,t2=-
,t2=-![]() ,
,
∴Q1=(0,![]() ),Q2(0,-
),Q2(0,-![]() )
)

(2)解:![]() :
:![]() 可化为
可化为
![]() ,
,
∴顶点M![]() ,
,
又∵抛物线![]() 与抛物线
与抛物线![]() 关于直线x=a对称,由对称性知:
关于直线x=a对称,由对称性知:
抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
又∵抛物线![]() 交y轴于点 P (0,-2m),
交y轴于点 P (0,-2m),
则有 ![]() ,
,
∴![]()
而直线x=a唯一,
∴![]() ,
,
解得,![]()
所以有![]() ,
,
解得,![]()


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则![]() 的值等于( )
的值等于( )
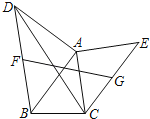
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
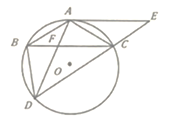
【题目】如图,在平行四边形ABCD中,连接AC,做△ABC的外接圆⊙O,延长EC交⊙O于点D,连接BD、AD,BC与AD交于点F分,∠ABC=∠ADB。
(1)求证:AE是⊙O的切线;
(2)若AE=12,CD=10,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外线投资是篮球队常规训练的重要项目之一,下列图表中数据是甲乙丙三从每从十次投篮测试的成绩,测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
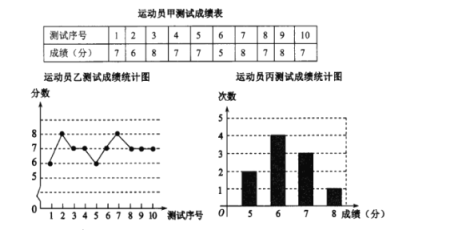
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三从中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
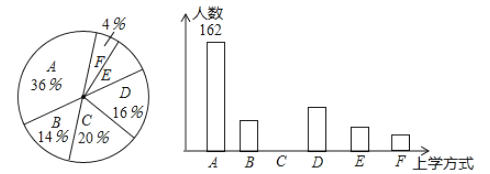
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系,根据图象,下列说法正确的是( )
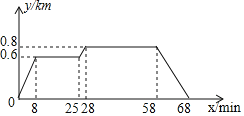
A.小明吃早餐用了25min
B.食堂到图书馆的距离为0.6km
C.小明读报用了30min
D.小明从图书馆回家的速度为0.8km/min
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com