
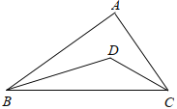
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 内,且
内,且![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作直线
作直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 与
与![]() 相似,则线段
相似,则线段![]() 的长为( )
的长为( )
A.5B.![]() C.5或
C.5或![]() D.6
D.6
【答案】B
【解析】
分△APQ∽△ABC,△APQ∽△ACB两种情况,结合相似三角形的性质和三角形内切圆求解即可.
解:若△APQ∽△ABC,
∴∠APQ=∠ABC,
∴PQ∥BC,![]() ,
,
∴∠PDB=∠DBC,
∵BD平分∠ABC,
∴∠PBD=∠CBD,
∴∠PBD =∠PDB,
∴PB=PD,同理,DQ=CQ,
∵![]() ,
,![]() ,
,![]() ,
,
∴BC=![]() ,
,
设AP=x,根据![]() 得
得![]() ,
,
∴AQ=![]() ,
,
∴PB=PD=8-x,CQ=DQ=6-![]() ,
,
∴PQ=PD+QD=![]() ,
,
∴![]() ,即
,即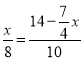 ,
,
解得:x=![]() ,
,
∴PQ=![]() ;
;
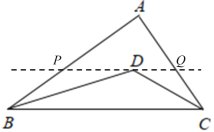
若△APQ∽△ACB,
则![]() ,
,
由题意知:D为△ABC的内心,设△ABC的内切圆交AB于M,交AC于N,
可知四边形AMDN为正方形,
∴∠A=∠AMD=∠AND=∠MDN=90°,
∴AM∥DN,AN∥DM,
∴∠MPD=∠NDQ,∠MDP=∠NQD,
∴△MPD∽△NDQ,
∴![]() ,
,
∵AB=8,AC=6,BC=10,
∴DM=DN=![]() =2,
=2,
∴AM=AN=2,
设PM=x,则![]() ,
,
∴NQ=![]() ,
,
∵![]() ,即
,即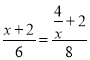 ,
,
解得:x=![]() 或-2(舍),
或-2(舍),
∴AP=![]() +2=
+2=![]() ,
,
∴PQ=AP×BC÷AC=![]() ×10÷6=
×10÷6=![]() .
.

综上:PQ的值为![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.



(1)在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
(2)当AP⊥EF时,求出此时t的值
(3)以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=_____.
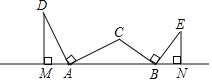
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.
x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.
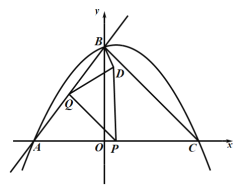
(1)求抛物线的解析式;
(2)当点D在抛物线上时,求点P的坐标.
(3)设点P的横坐标为x,△PDQ与△ABC的重叠部分的面积为S
①直接写出S与x的函数关系式;
②当△BDQ为直角三角形时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
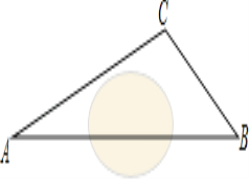
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《流浪地球》的销量急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次购进该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?每套进价多少元?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店店主期盼最高日利润达到2500元,他的愿望能实现吗?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A′BC′,若反比例函数![]() 的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
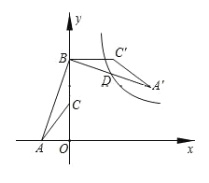
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com