
ЁОЬтФПЁППЦЛУаЁЫЕЁЖСїРЫЕиЧђЁЗЕФЯњСПМБОчЩЯЩ§ЃЎЮЊгІЖдетжжБфЛЏЃЌФГЭјЕъЗжБ№ЛЈ20000дЊКЭ30000дЊЯШКѓСНДЮЙКНјИУаЁЫЕЃЌЕкЖўДЮЕФЪ§СПБШЕквЛДЮЖр500ЬзЃЌЧвСНДЮНјМлЯрЭЌЃЎ
ЃЈ1ЃЉИУПЦЛУаЁЫЕЕквЛДЮЙКНјЖрЩйЬзЃПУПЬзНјМлЖрЩйдЊЃП
ЃЈ2ЃЉИљОнвдЭљОбщЃКЕБЯњЪлЕЅМлЪЧ25дЊЪБЃЌУПЬьЕФЯњЪлСПЪЧ250ЬзЃЛЯњЪлЕЅМлУПЩЯеЧ1дЊЃЌУПЬьЕФЯњЪлСПОЭМѕЩй10ЬзЃЎЭјЕъвЊЧѓУПЬзЪщЕФРћШѓВЛЕЭгк10дЊЧвВЛИпгк18дЊЃЎ
ЂйжБНгаДГіЭјЕъЯњЪлИУПЦЛУаЁЫЕУПЬьЕФЯњЪлСПyЃЈЬзЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЂкЭјЕъЕъжїЦкХЮзюИпШеРћШѓДяЕН2500дЊЃЌЫћЕФдИЭћФмЪЕЯжТ№?ЧыФуЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉИУПЦЛУаЁЫЕЕквЛДЮЙКНј1000ЬзЃЛУПЬзНјМў20дЊЃЛЃЈ2ЃЉЂйyЃНЉ10x+500ЃЈ30ЁмxЁм38ЃЉЃЛЂкЫћЕФдИЭћВЛФмЪЕЯжЃЌРэгЩМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшИУПЦЛУаЁЫЕЕквЛДЮЙКНјmЬзЃЌИљОнЬтвтСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйИљОнЬтвтСаКЏЪ§ЙиЯЕЪНЃЌИљОнУПЬзЪщЕФРћШѓВЛЕЭгк10дЊЧвВЛИпгк18дЊЧѓГіxЕФШЁжЕЗЖЮЇЃЛ
ЂкЩшУПЬьПлГ§ОшдљКѓПЩЛёЕУРћШѓЮЊwдЊЃЎИљОнЬтвтЕУЕНwгыxжЎМфЕФКЏЪ§ЙиЯЕЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЩшИУПЦЛУаЁЫЕЕквЛДЮЙКНјmЬзЃЌ
дђ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрmЃН1000ЃЌ
ОМьбщЃЌmЃН1000ЪЧдЗНГЬЕФНтЃЌ
![]() дЊ/ЬзЃЌ
дЊ/ЬзЃЌ
Д№ЃКИУПЦЛУаЁЫЕЕквЛДЮЙКНј1000ЬзЃЛУПЬзНјМў20дЊЃЛ
ЃЈ2ЃЉЂйгЩЬтвтЕУ
yЃН250Љ10(xЉ25)ЃНЉ10x+500ЃЌ
Ёп10Ёмx-20Ём18ЃЌ
Ёр30ЁмxЁм38ЃЌ
ЁрyЃНЉ10x+500ЃЈ30ЁмxЁм38ЃЉЃЛ
ЂкЩшУПЬьПЩЛёЕУРћШѓЮЊwдЊЃЌгЩЬтвтЕУ
wЃН(xЉ20)(Љ10x+500)
ЃНЉ10x2+700xЉ10000
=Љ10(x-35)2+2250ЃЈ30ЁмxЁм38ЃЉЃЌ
Ёп-10<0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЌ
Ёп30ЁмxЁм38ЃЌ
Ёрx=35ЪБЃЌwзюДѓ=2250<2500ЃЌ
ЁрЫћЕФдИЭћВЛФмЪЕЯжЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЈ-1ЃЌ3ЃЉЃЌBЃЈ3ЃЌ
ЕФЭМЯѓНЛгкAЃЈ-1ЃЌ3ЃЉЃЌBЃЈ3ЃЌ![]() ЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
ЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
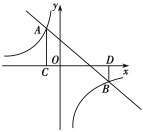
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§МАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPдкжБЯп![]() ЩЯЃЌЧвSЁїACPЃН2SЁїBDPЃЌЧѓЕуPЕФзјБъЃЎ
ЩЯЃЌЧвSЁїACPЃН2SЁїBDPЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ФкЃЌЧв
ФкЃЌЧв![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() гы
гы![]() ЯрЫЦЃЌдђЯпЖЮ
ЯрЫЦЃЌдђЯпЖЮ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.5B.![]() C.5Лђ
C.5Лђ![]() D.6
D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
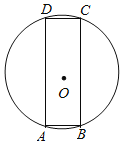
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЁбOЕФФкНгОиаЮЃЌНЋОиаЮABCDбизХжБЯпBCЗелЃЌЕуAЁЂЕуDЕФЖдгІЕуЗжБ№ЮЊAЁфЁЂDЁфЃЌШчЙћжБЯпAЁфDЁфгыЁбOЯрЧаЃЌФЧУД![]() ЕФжЕЮЊ_____ЃЎ
ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1ЃНmx+nгыЗДБШР§КЏЪ§y2ЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕуAЃЈaЃЌ4ЃЉКЭЕуBЃЈ8ЃЌ1ЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕуDЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕуAЃЈaЃЌ4ЃЉКЭЕуBЃЈ8ЃЌ1ЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕуDЃЎ
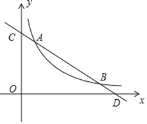
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓЃЌЕБxЃО0ЪБЃЌжБНгаДГіy1>y2ЕФНтМЏЃЛ
ЃЈ3ЃЉШєЕуPЪЧxжсЩЯвЛЖЏЕуЃЌЕБЁїCODгыЁїADPЯрЫЦЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊБпГЄЮЊ5ЕФСтаЮABCDжаЃЌЖдНЧЯпACГЄЮЊ6ЃЌЕуEдкЖдНЧЯпBDЩЯЧвtanЁЯEAC=![]() ЃЌдђBEЕФГЄЮЊ_____ЃЎ
ЃЌдђBEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.СЫНтФГаЭЕМЕЏЩБЩЫСІЕФЧщПігІЪЙгУШЋУцЕїВщ
B.ПЩФмадЪЧ1%ЕФЪТМўдквЛДЮЪдбщжавЛЖЈВЛЛсЗЂЩњ
C.вЛзщЪ§Он3ЁЂ6ЁЂ6ЁЂ7ЁЂ9ЕФжкЪ§ЪЧ6
D.МзЃЌввСНШЫдкЯрЭЌЕФЬѕМўЯТИїЩфЛї10ДЮЃЌЫћУЧГЩМЈЕФЦНОљЪ§ЯрЭЌЃЌЗНВюЗжБ№ЪЧ![]() =0.3ЃЌ
=0.3ЃЌ![]() =0.4ЃЌдђввЕФГЩМЈИќЮШЖЈ
=0.4ЃЌдђввЕФГЩМЈИќЮШЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНаЃИїбЁХЩ10УћбЇЩњВЮМгЁАУРРіЬЉжнЯчЭСЗчЧщжЊЪЖЁБДѓШќдЄШќЃЎИїВЮШќбЁЪжЕФГЩМЈШчЯТЃК
МзаЃЃК93ЃЌ98ЃЌ89ЃЌ93ЃЌ 95ЃЌ96ЃЌ 93ЃЌ96ЃЌ98ЃЌ 99ЃЛ
вваЃЃК93ЃЌ94ЃЌ88ЃЌ91ЃЌ92ЃЌ93ЃЌ100ЃЌ 98ЃЌ98ЃЌ93ЃЎ
ЭЈЙ§ећРэЃЌЕУЕНЪ§ОнЗжЮіБэШчЯТЃК
бЇаЃ | зюИпЗж | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ | ЗНВю |
МзаЃ | 99 | a | 95.5 | 93 | 8.4 |
вваЃ | 100 | 94 | b | 93 | c |
ЃЈ1ЃЉЬюПеЃКa = ЃЌb = ЃЛ
ЃЈ2ЃЉЧѓГіБэжаcЕФжЕЃЌФуШЯЮЊФФЫљбЇаЃДњБэЖгГЩМЈКУЃПЧыаДГіСНЬѕФуШЯЮЊИУЖгГЩМЈКУЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
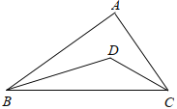
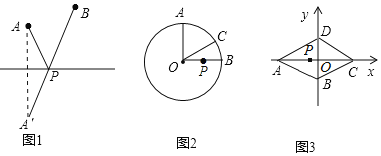
ЁОЬтФПЁПдФЖСВФСЯЃКЁАзюжЕЮЪЬтЁБЪЧЪ§бЇжаЕФвЛРрНЯОпЬєеНадЕФЮЪЬтЃЎЦфЪЕЃЌЪ§бЇЪЗЩЯвВгаВЛЩйЯрЙиЕФЙЪЪТЃЌШчЯТМДЮЊЦфжаНЯЮЊОЕфЕФвЛдђЃККЃТзЪЧЙХЯЃРАОЋЭЈЪ§бЇЁЂЮяРэЕФбЇепЃЌЯрДЋгаЮЛНЋОќдјЯђЫћЧыНЬвЛИіЮЪЬтЉЉШчЭМ1ЃЌДгAЕуГіЗЂЃЌЕНБЪжБЕФКгАЖlШЅвћТэЃЌШЛКѓдйШЅBЕиЃЌзпЪВУДбљЕФТЗЯпзюЖЬФиЃПКЃТзЧсЫЩЕиИјГіСЫД№АИЃКзїЕуAЙигкжБЯпlЕФЖдГЦЕуAЁфЃЌСЌНгAЁфBНЛlгкЕуPЃЌдђPA+PBЃНAЁфB ЕФжЕзюаЁЃЎ
НтД№ЮЪЬтЃК
ЃЈ1ЃЉШчЭМ2ЃЌЁбOЕФАыОЖЮЊ2ЃЌЕуAЁЂBЁЂCдкЁбOЩЯЃЌOAЁЭOBЃЌЁЯAOCЃН60ЁуЃЌPЪЧOBЩЯвЛЖЏЕуЃЌЧѓPA+PCЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌвбжЊСтаЮABCDЕФБпГЄЮЊ6ЃЌЁЯDABЃН60ЁуЃЎНЋДЫСтаЮЗХжУгкЦНУцжБНЧзјБъЯЕжаЃЌИїЖЅЕуЧЁКУдкзјБъжсЩЯЃЎЯжгавЛЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШЃЌбиAЁњCЕФЗНЯђЃЌЯђЕуCдЫЖЏЃЎЕБЕНДяЕуCКѓЃЌСЂМДвдЯрЭЌЕФЫйЖШЗЕЛиЃЌЗЕЛиЭОжаЃЌЕБдЫЖЏЕНxжсЩЯФГвЛЕуMЪБЃЌСЂМДвдУПУы1ИіЕЅЮЛЕФЫйЖШЃЌбиMЁњBЕФЗНЯђЃЌЯђЕуBдЫЖЏЃЎЕБЕНДяЕуBЪБЃЌећИідЫЖЏЭЃжЙЃЎ
ЂйЮЊЪЙЕуPФмдкзюЖЬЕФЪБМфФкЕНДяЕуBДІЃЌдђЕуMЕФЮЛжУгІШчКЮШЗЖЈЃП
ЂкдкЂйЕФЬѕМўЯТЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЁїPABЕФУцЛ§ЮЊSЃЌдкећИідЫЖЏЙ§ГЬжаЃЌЪдЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com