
【题目】如图,一次函数y1=mx+n与反比例函数y2=![]() (x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
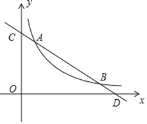
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当x>0时,直接写出y1>y2的解集;
(3)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
【答案】(1)y1=﹣![]() x+5, y2=
x+5, y2=![]() ;(2)2<x<8;(3)点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
;(2)2<x<8;(3)点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
【解析】
(1)先将点B代入反比例函数解析式中求出反比例函数的解析式,然后进一步求出A的坐标,再将A,B代入一次函数中求一次函数解析式即可;
(2)根据图象和两函数的交点即可写出y1>y2的解集;
(3)先求出C,D的坐标,从而求出CD,AD,OD的长度,然后分两种情况:当![]() 时,△COD∽△APD;当
时,△COD∽△APD;当![]() 时,△COD∽△PAD,分别利用相似三角形的性质进行讨论即可.
时,△COD∽△PAD,分别利用相似三角形的性质进行讨论即可.
解:(1)把B(8,1)代入反比例函数![]() 中,
中,
则![]() ,解得
,解得![]()
∴反 比 例 函 数 的 关 系 式 为 ![]() ,
,
∵点 A(a,4)在![]() 图象上,
图象上,
∴ a=![]() =2,即A(2,4)
=2,即A(2,4)
把A(2,4),B(8,1)两点代入y1=mx+n中得
![]() 解得:
解得: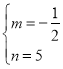 ,
,
所以直线AB的解析式为:y1=﹣![]() x+5;反比例函数的关系式为y2=
x+5;反比例函数的关系式为y2=![]() ,
,
(2)由图象可得,当x>0时,y1>y2的解集为2<x<8.
(3)由(1)得直线AB的解析式为y1=﹣![]() x+5,
x+5,
当x=0时,y=5,
∴ C(0,5),
∴ OC=5,
当y=0时,x=10,
∴D点坐标为(10,0)
∴ OD=10,
∴ CD=![]() =
=![]()
∵A(2,4),
∴ AD=![]() =4
=4![]()
设P点坐标为(a,0),由题可知,点P在点D左侧,则PD=10﹣a
由∠CDO=∠ADP可得
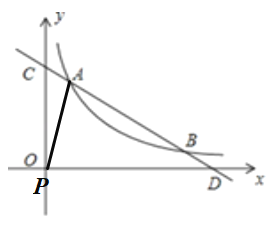
①当![]() 时,
时,![]() ,如图1
,如图1

此时![]() ,
,
∴![]() ,解得a=2,
,解得a=2,
故点P坐标为(2,0)
②当![]() 时,
时,![]() ,如图2
,如图2
当时,![]() ,
,
∴![]() ,解得a=0,
,解得a=0,
即点P的坐标为(0,0)
因此,点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
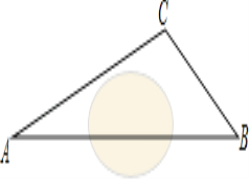
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
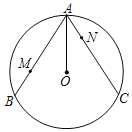
【题目】如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《流浪地球》的销量急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次购进该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?每套进价多少元?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店店主期盼最高日利润达到2500元,他的愿望能实现吗?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
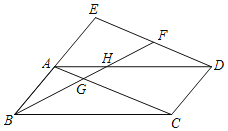
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使得AE=AB,联结DE、AC.点F在线段DE上,联结BF,分别交AC、AD于点G、H.
(1)求证:BG=GF;
(2)如果AC=2AB,点F是DE的中点,求证:AH2=GHBH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com