
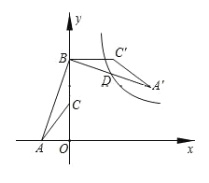
【题目】如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A′BC′,若反比例函数![]() 的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
【答案】![]() .
.
【解析】
作A′H⊥y轴于H.证明△AOB≌△BHA′(AAS),推出OA=BH,OB=A′H,求出点A′坐标,再利用中点坐标公式求出点D坐标即可解决问题.
作A′H⊥y轴于H.
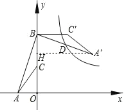
∵∠AOB=∠A′HB=∠ABA′=90°,
∴∠ABO+∠A′BH=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠A′BH,
∵BA=BA′,
∴△AOB≌△BHA′(AAS),
∴OA=BH,OB=A′H,
∵点A的坐标是(2,0),点B的坐标是(0,6),
∴OA=2,OB=6,
∴BH=OA=2,A′H=OB=6,
∴OH=4,
∴A′(6,4),
∵BD=A′D ,
∴D(3,5),
∵反比例函数的图象经过点D,
∴这个反比例函数的解析式![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解某型导弹杀伤力的情况应使用全面调查
B.可能性是1%的事件在一次试验中一定不会发生
C.一组数据3、6、6、7、9的众数是6
D.甲,乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是![]() =0.3,
=0.3,![]() =0.4,则乙的成绩更稳定
=0.4,则乙的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校各选派10名学生参加“美丽泰州乡土风情知识”大赛预赛.各参赛选手的成绩如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通过整理,得到数据分析表如下:
学校 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你认为哪所学校代表队成绩好?请写出两条你认为该队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是( )
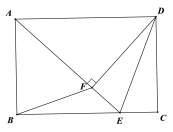
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
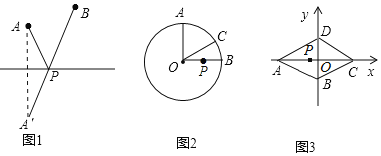
【题目】阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题﹣﹣如图1,从A点出发,到笔直的河岸l去饮马,然后再去B地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B 的值最小.
解答问题:
(1)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(2)如图3,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.
①为使点P能在最短的时间内到达点B处,则点M的位置应如何确定?
②在①的条件下,设点P的运动时间为t(s),△PAB的面积为S,在整个运动过程中,试求S与t之间的函数关系式,并指出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com