
ЁОЬтФПЁПЬНОПЃКШчЭМ1КЭЭМ2ЃЌЫФБпаЮABCDжаЃЌвбжЊABЃНADЃЌЁЯBADЃН90ЁуЃЌЕуEЁЂFЗжБ№дкBCЁЂCDЩЯЃЌЁЯEAFЃН45ЁуЃЎ
ЃЈ1ЃЉЂйШчЭМ1ЃЌШєЁЯBЁЂЁЯADCЖМЪЧжБНЧЃЌАбЁїABEШЦЕуAФцЪБеыа§зЊ90ЁужСЁїADGЃЌЪЙABгыADжиКЯЃЌжБНгаДГіЯпЖЮBEЁЂDFКЭEFжЎМфЕФЪ§СПЙиЯЕЁЁ ЁЁЃЛ
ЂкШчЭМ2ЃЌШєЁЯBЁЂЁЯDЖМВЛЪЧжБНЧЃЌЕЋТњзуЁЯB+ЁЯDЃН180ЁуЃЌЯпЖЮBEЁЂDFКЭEFжЎМфЕФНсТлЪЧЗёШдШЛГЩСЂЃЌШєГЩСЂЃЌЧыаДГіжЄУїЙ§ГЬЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЭиеЙЃКШчЭМ3ЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃН2![]() ЃЎЕуDЁЂEОљдкБпBCБпЩЯЃЌЧвЁЯDAEЃН45ЁуЃЌШєBDЃН1ЃЌЧѓDEЕФГЄЃЎ
ЃЎЕуDЁЂEОљдкБпBCБпЩЯЃЌЧвЁЯDAEЃН45ЁуЃЌШєBDЃН1ЃЌЧѓDEЕФГЄЃЎ
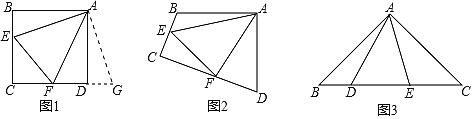
ЁОД№АИЁПЃЈ1ЃЉЂйEFЃНBE+DFЃЛЂкГЩСЂЃЌРэгЩЯъМћНтЮіЃЛЃЈ2ЃЉDEЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОна§зЊЕФаджЪЕУГіAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌBEЃНDGЃЌЧѓГіЁЯEAFЃНЁЯGAFЃН45ЁуЃЌИљОнSASЭЦГіЁїEAFЁеЁїGAFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіEFЃНGFЃЌМДПЩЧѓГіД№АИЃЛ
ЂкИљОна§зЊЕФаджЪзїИЈжњЯпЃЌЕУГіAEЃНAGЃЌЁЯBЃНЁЯADGЃЌЁЯBAEЃНЁЯDAGЃЌЧѓГіCЁЂDЁЂGдквЛЬѕжБЯпЩЯЃЌИљОнSASЭЦГіЁїEAFЁеЁїGAFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіEFЃНGFЃЌМДПЩЧѓГіД№АИЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌЭЌРэзїа§зЊШ§НЧаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮаджЪКЭЙДЙЩЖЈРэЧѓГіЁЯABCЃНЁЯCЃН45ЁуЃЌBCЃН4ЃЌИљОна§зЊЕФаджЪЕУГіAFЃНAEЃЌЁЯFBAЃНЁЯCЃН45ЁуЃЌЁЯBAFЃНЁЯCAEЃЌЧѓГіЁЯFADЃНЁЯDAEЃН45ЁуЃЌжЄЁїFADЁеЁїEADЃЌИљОнШЋЕШЕУГіDFЃНDEЃЌЩшDEЃНxЃЌдђDFЃНxЃЌBFЃНCEЃН3ЉxЃЌИљОнЙДЙЩЖЈРэЕУГіЗНГЬЃЌЧѓГіxМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпАбЁїABEШЦЕуAФцЪБеыа§зЊ90ЁужСЁїADGЃЌЪЙABгыADжиКЯЃЌ
ЁрAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌBEЃНDGЃЌЁЯBЃНЁЯADGЃН90ЁуЃЌ
ЁпЁЯADCЃН90ЁуЃЌ
ЁрЁЯADC+ЁЯADGЃН90Ёу
ЁрFЁЂDЁЂGЙВЯпЃЌ
ЁпЁЯBADЃН90ЁуЃЌЁЯEAFЃН45ЁуЃЌ
ЁрЁЯBAE+ЁЯDAFЃН45ЁуЃЌ
ЁрЁЯDAG+ЁЯDAFЃН45ЁуЃЌ
МДЁЯEAFЃНЁЯGAFЃН45ЁуЃЌ
дкЁїEAFКЭЁїGAFжаЃЌ
Ёп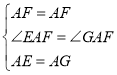 ЃЌ
ЃЌ
ЁрЁїEAFЁеЁїGAFЃЈSASЃЉЃЌ
ЁрEFЃНGFЃЌ
ЁпBEЃНDGЃЌ
ЁрEFЃНGFЃНDF+DGЃНBE+DFЃЌ
ЙЪД№АИЮЊЃКEFЃНBE+DFЃЛ
ЂкГЩСЂЃЌ
РэгЩЃКШчЭМ2ЃЌАбЁїABEШЦAЕуа§зЊЕНЁїADGЃЌЪЙABКЭADжиКЯЃЌ

дђAEЃНAGЃЌЁЯBЃНЁЯADGЃЌЁЯBAEЃНЁЯDAGЃЌ
ЁпЁЯB+ЁЯADCЃН180ЁуЃЌ
ЁрЁЯADC+ЁЯADGЃН180ЁуЃЌ
ЁрCЁЂDЁЂGдквЛЬѕжБЯпЩЯЃЌ
гыЂйЭЌРэЕУЃЌЁЯEAFЃНЁЯGAFЃН45ЁуЃЌ
дкЁїEAFКЭЁїGAFжаЃЌ
Ёп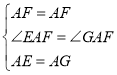 ЃЌ
ЃЌ
ЁрЁїEAFЁеЁїGAFЃЈSASЃЉЃЌ
ЁрEFЃНGFЃЌ
ЁпBEЃНDGЃЌ
ЁрEFЃНGFЃНBE+DFЃЛ
ЃЈ2ЃЉНтЃКЁпЁїABCжаЃЌABЃНACЃН2![]() ЃЌЁЯBACЃН90ЁуЃЌ
ЃЌЁЯBACЃН90ЁуЃЌ
ЁрЁЯABCЃНЁЯCЃН45ЁуЃЌ
гЩЙДЙЩЖЈРэЕУЃКBCЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ШчЭМ3ЃЌАбЁїAECШЦAЕуа§зЊЕНЁїAFBЃЌЪЙABКЭACжиКЯЃЌСЌНгDFЃЌ
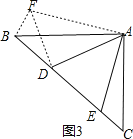
дђAFЃНAEЃЌЁЯFBAЃНЁЯCЃН45ЁуЃЌЁЯBAFЃНЁЯCAEЃЌ
ЁпЁЯDAEЃН45ЁуЃЌ
ЁрЁЯFADЃНЁЯFAB+ЁЯBADЃНЁЯCAE+ЁЯBADЃНЁЯBACЉЁЯDAEЃН90ЁуЉ45ЁуЃН45ЁуЃЌ
ЁрЁЯFADЃНЁЯDAEЃН45ЁуЃЌ
дкЁїFADКЭЁїEADжа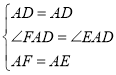 ЃЌ
ЃЌ
ЁрЁїFADЁеЁїEADЃЈSASЃЉЃЌ
ЁрDFЃНDEЃЌ
ЩшDEЃНxЃЌдђDFЃНxЃЌ
ЁпBCЃН4ЃЌ
ЁрBFЃНCEЃН4Љ1ЉxЃН3ЉxЃЌ
ЁпЁЯFBAЃН45ЁуЃЌЁЯABCЃН45ЁуЃЌ
ЁрЁЯFBDЃН90ЁуЃЌ
гЩЙДЙЩЖЈРэЕУЃКDF2ЃНBF2+BD2ЃЌ
x2ЃНЃЈ3ЉxЃЉ2+12ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
МДDEЃН![]() ЃЎ
ЃЎ


 СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ
СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ УЯНЈЦНДэЬтБОЯЕСаД№АИ
УЯНЈЦНДэЬтБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпyЃН![]() xгыЫЋЧњЯпyЃН
xгыЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЉНЛгкAЁЂBСНЕуЃЌAЕуЕФКсзјБъЮЊ3ЃЌдђЯТСаНсТлЃКЂйkЃН6ЃЛЂкAЕугыBЕуЙигкдЕуOжааФЖдГЦЃЛЂлЙигкxЕФВЛЕШЪН
ЃЈkЃО0ЃЉНЛгкAЁЂBСНЕуЃЌAЕуЕФКсзјБъЮЊ3ЃЌдђЯТСаНсТлЃКЂйkЃН6ЃЛЂкAЕугыBЕуЙигкдЕуOжааФЖдГЦЃЛЂлЙигкxЕФВЛЕШЪН![]() ЃМ0ЕФНтМЏЮЊxЃМЉ3Лђ0ЃМxЃМ3ЃЛЂмШєЫЋЧњЯпyЃН
ЃМ0ЕФНтМЏЮЊxЃМЉ3Лђ0ЃМxЃМ3ЃЛЂмШєЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЉЩЯгавЛЕуCЕФзнзјБъЮЊ6ЃЌдђЁїAOCЕФУцЛ§ЮЊ8ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЃЈЁЁЁЁЃЉ
ЃЈkЃО0ЃЉЩЯгавЛЕуCЕФзнзјБъЮЊ6ЃЌдђЁїAOCЕФУцЛ§ЮЊ8ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЃЈЁЁЁЁЃЉ
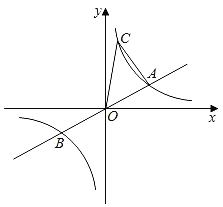
A.4ИіB.3ИіC.2ИіD.1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
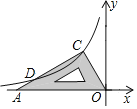
ЁОЬтФПЁПШчЭМЃЌАбвЛПщКЌ30ЁуНЧЕФШ§НЧАхЕФжБНЧЖЅЕуЗХдкЗДБШР§КЏЪ§y=-![]() ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЕФЕуCДІЃЌСэСНИіЖЅЕуЗжБ№ТфдкдЕуOКЭxжсЕФИКАыжсЩЯЕФЕуAДІЃЌЧвЁЯCAO=30ЁуЃЌдђACБпгыИУКЏЪ§ЭМЯѓЕФСэвЛНЛЕуDЕФзјБъЮЊ__________ЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЕФЕуCДІЃЌСэСНИіЖЅЕуЗжБ№ТфдкдЕуOКЭxжсЕФИКАыжсЩЯЕФЕуAДІЃЌЧвЁЯCAO=30ЁуЃЌдђACБпгыИУКЏЪ§ЭМЯѓЕФСэвЛНЛЕуDЕФзјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020Фъ3дТ24ШеЃЌЙЄаХВПЗЂВМЁЖЙигкЭЦЖЏ![]() МгПьЗЂеЙЕФЭЈжЊЁЗЃЌШЋСІЭЦНј
МгПьЗЂеЙЕФЭЈжЊЁЗЃЌШЋСІЭЦНј![]() ЭјТчНЈЩшЁЂгІгУЭЦЙуЁЂММЪѕЗЂеЙКЭАВШЋБЃеЯЃЎЙЄаХВПЬсГіЃЌвЊХрг§аТаЭЯћЗбФЃЪНЃЌМгПьгУЛЇЯђ
ЭјТчНЈЩшЁЂгІгУЭЦЙуЁЂММЪѕЗЂеЙКЭАВШЋБЃеЯЃЎЙЄаХВПЬсГіЃЌвЊХрг§аТаЭЯћЗбФЃЪНЃЌМгПьгУЛЇЯђ![]() ЧЈвЦЃЌЭЦЖЏЁА
ЧЈвЦЃЌЭЦЖЏЁА![]() вНСЦНЁПЕЁБДДаТЗЂеЙЃЌЪЕЪЉЁА
вНСЦНЁПЕЁБДДаТЗЂеЙЃЌЪЕЪЉЁА![]() ЙЄвЕЛЅСЊЭјЁБ512ЙЄГЬЃЌДйНјЁА
ЙЄвЕЛЅСЊЭјЁБ512ЙЄГЬЃЌДйНјЁА![]() ГЕСЊЭјЁБаЭЌЗЂеЙЃЌЙЙНЈ
ГЕСЊЭјЁБаЭЌЗЂеЙЃЌЙЙНЈ![]() гІгУЩњЬЌЯЕЭГЃЎЯжЁА
гІгУЩњЬЌЯЕЭГЃЎЯжЁА![]() ЭјТчЁБвбГЩЮЊвЛИіШШУХДЪЛуЃЌФГаЃЮЊСЫНтОХФъМЖбЇЩњЖдЁА
ЭјТчЁБвбГЩЮЊвЛИіШШУХДЪЛуЃЌФГаЃЮЊСЫНтОХФъМЖбЇЩњЖдЁА![]() ЭјТчЁБЕФСЫНтГЬЖШЃЌЖдОХФъМЖбЇЩњааСЫвЛДЮВтЪд(вЛЙВ10ЕРЬтД№Жд1ЕРЕУ1ЗжЃЌТњЗж10Зж)ЃЌВтЪдНсЪјКѓЫцЛњГщШЁСЫВПЗжбЇЩњЕФГЩМЈећРэЗжЮіЃЌЛцжЦГіШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
ЭјТчЁБЕФСЫНтГЬЖШЃЌЖдОХФъМЖбЇЩњааСЫвЛДЮВтЪд(вЛЙВ10ЕРЬтД№Жд1ЕРЕУ1ЗжЃЌТњЗж10Зж)ЃЌВтЪдНсЪјКѓЫцЛњГщШЁСЫВПЗжбЇЩњЕФГЩМЈећРэЗжЮіЃЌЛцжЦГіШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
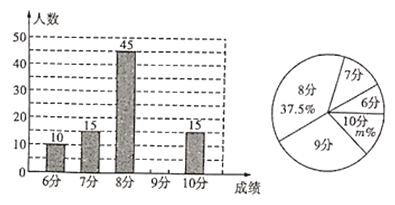
ЃЈ1ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЌЩШаЮЭГМЦЭМжа![]() ЁЁЁЁЁЁЁЁ__ЃЛ
ЁЁЁЁЁЁЁЁ__ЃЛ
ЃЈ2ЃЉЫљЕїВщбЇЩњГЩМЈЕФжкЪ§ЪЧ_ЁЁЁЁЁЁЁЁ____ЗжЃЌЦНОљЪ§ЪЧ_ЁЁЁЁЁЁЁЁЗжЃЛ
ЃЈ3ЃЉШєИУаЃОХФъМЖбЇЩњга![]() ШЫЃЌЧыЙРМЦЕУЗжВЛЩйгк
ШЫЃЌЧыЙРМЦЕУЗжВЛЩйгк![]() ЗжЕФгаЖрЩйШЫЃП
ЗжЕФгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕузјБъAЃЈЉ1ЃЌ3ЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈЉ4ЃЌ0ЃЉЃЌжБЯпy2=mx+nЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃКЂй2aЉb=0ЃЛЂкabcЃМ0ЃЛЂлХзЮяЯпгыxжсЕФСэвЛИіНЛЕузјБъЪЧЃЈ3ЃЌ0ЃЉЃЛЂмЗНГЬax2+bx+cЉ3=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЛЂнЕБЉ4ЃМxЃМЉ1ЪБЃЌдђy2ЃМy1ЃЎ
Цфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂл B. ЂйЂлЂн C. ЂйЂмЂн D. ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёФъЪЧЭбЦЖЙЅМсзюКѓвЛФъЃЌФГеђФтаовЛЬѕСЌЭЈЦЖРЇЩНЧјДхЕФЙЋТЗЃЌЯжгаМзЁЂввСНИіЙЄГЬЖгЃЎШєМзЁЂввКЯзїЃЌ36ЬьПЩвдЭъГЩЃЌашгУ600ЭђдЊЃЛШєМзЕЅЖРзі20ЬьКѓЃЌЪЃЯТЕФгЩввзіЃЌЛЙаш40ЬьВХФмЭъГЩЃЌетбљЫљаш550ЭђдЊЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНЖгЕЅЖРЭъГЩДЫЯюЙЄГЬИїашЖрЩйЬьЃП
ЃЈ2ЃЉЧѓМзЁЂввСНЖгЕЅЖРЭъГЩДЫЯюЙЄГЬИїашЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌCЪЧАыдВOЩЯвЛЕуЃЈВЛгыЕуAЁЂBжиКЯЃЉЃЌDЪЧ![]() ЕФжаЕуЃЌDEЁЭABгкЕуEЃЌЙ§ЕуCзїАыдВOЕФЧаЯпЃЌНЛEDЕФбгГЄЯпгкЕуFЃЎ
ЕФжаЕуЃЌDEЁЭABгкЕуEЃЌЙ§ЕуCзїАыдВOЕФЧаЯпЃЌНЛEDЕФбгГЄЯпгкЕуFЃЎ
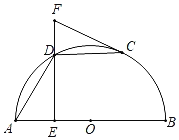
ЃЈ1ЃЉЧѓжЄЃКЁЯFCDЃНЁЯADEЃЛ
ЃЈ2ЃЉЬюПеЃК
ЂйЕБЁЯFCDЕФЖШЪ§ЮЊЁЁ ЁЁЪБЃЌЫФБпаЮOADCЪЧСтаЮЃЛ
ЂкШєABЃН2![]() ЃЌЕБCFЁЮABЪБЃЌDFЕФГЄЮЊЁЁ ЁЁЃЎ
ЃЌЕБCFЁЮABЪБЃЌDFЕФГЄЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌACЃНBCЃН4ЃЌЁЯCЃН90ЁуЃЌDЪЧBCБпЩЯвЛЕуЃЌЧвCDЃН3BDЃЌСЌНгADЃЌАбЁїACDбиADЗелЃЌЕУЕНЁїADC'ЃЌDCЁфгыABНЛгкЕуEЃЌСЌНгBCЁфЃЌдђЁїBDC'ЕФУцЛ§ЮЊЃЈ ЃЉ
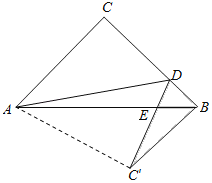
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
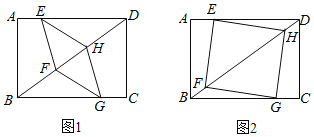
ЁОЬтФПЁПОиаЮABCDЃЌAB=6ЃЌBC=8ЃЌЫФБпаЮEFGHЕФЖЅЕуEЁЂGдкОиаЮЕФБпADЁЂBCЩЯЃЛЖЅЕуFЁЂHдкОиаЮЕФЖдНЧЯпBDЩЯЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЫФБпаЮEFGHЪЧЦНааЫФБпаЮЪБЃЌЧѓжЄЃКЁїDEHЁеЁїBGFЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЫФБпаЮEFGHЪЧе§ЗНаЮЪБЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com