
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式
(k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式![]() <0的解集为x<﹣3或0<x<3;④若双曲线y=
<0的解集为x<﹣3或0<x<3;④若双曲线y=![]() (k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
(k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
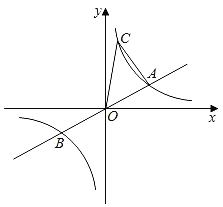
A.4个B.3个C.2个D.1个
【答案】A
【解析】
①由A点横坐标为3,代入正比例函数,可求得点A的坐标,继而求得k值;
②根据直线和双曲线的性质即可判断;
③结合图象,即可求得关于x的不等式![]() <0的解集;
<0的解集;
④过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC=S△OCD+S梯形AEDC-S△AOE=S梯形AEDC,由点C的纵坐标为6,可求得点C的坐标,继而求得答案.
①∵直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,A点的横坐标为3,
(k>0)交于A、B两点,A点的横坐标为3,
∴点A的纵坐标为:y=![]() ×3=2,
×3=2,
∴点A(3,2),
∴k=3×2=6,
故①正确;
②∵直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)是中心对称图形,
(k>0)是中心对称图形,
∴A点与B点关于原点O中心对称
,故②正确;
③∵直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,
(k>0)交于A、B两点,
∴B(﹣3,﹣2),
∴关于x的不等式![]() <0的解集为:x<﹣3或0<x<3,
<0的解集为:x<﹣3或0<x<3,
故③正确;
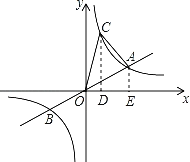
④过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,
∵点C的纵坐标为6,
∴把y=6代入y=![]() 得:x=1,
得:x=1,
∴点C(1,6),
∴S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=![]() ×(2+6)×(3﹣1)=8,故④正确;
×(2+6)×(3﹣1)=8,故④正确;
故选:A.


科目:初中数学 来源: 题型:
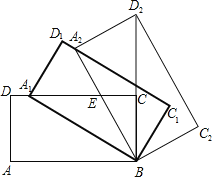
【题目】如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() =
=![]() ﹣1,求
﹣1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月24日《复仇者联盟4》在中国大陆上映.我市江北UME影城为加大宣传,决定在4月23日预售普通3D票400张和IMAX票100张,且预售中的IMAX的票价是普通3D票价的2倍.
(1)若影城的预售总额不低于21000元,则普通3D票的预售价格最少为多少元?
(2)影城计划在上映当天推出普通3D票3200张,IMAX票800张.由于预售的火爆,影城决定将普通3D票的价格在(1)中最低价格的基础上增加![]() %,而IMAX票价在(1)中IMAX票价上增加了a元,结果普通3D票的销售量比计划少2a%.IMAX票的销售量与计划保持一致,最终实际销售额与计划销售额相等,求a的值.
%,而IMAX票价在(1)中IMAX票价上增加了a元,结果普通3D票的销售量比计划少2a%.IMAX票的销售量与计划保持一致,最终实际销售额与计划销售额相等,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
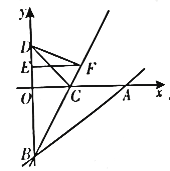
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
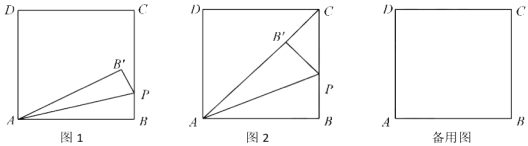
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
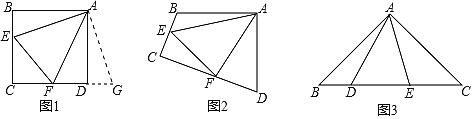
【题目】探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系 ;
②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() .点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com