
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
【答案】(1)①![]() ;②t=2或t=6或t=2
;②t=2或t=6或t=2![]() (2)见解析.
(2)见解析.
【解析】
(1)①先利用勾股定理求出AC长,再根据△APB≌△APB′,继而根据全等三角形的性质推导得出∠B=∠PB′C=90°,B′C= ![]() ,再证明
,再证明![]() ,根据相似三角形的性质求出PB′=2
,根据相似三角形的性质求出PB′=2![]() -4,由此即可求得答案;
-4,由此即可求得答案;
②根据题意分三种情况,分别画出图形,结合图形分别讨论求解即可;
(2)如图,根据∠PAM=45°以及翻折的性质可以证明得到△DAM≌△B′AM,从而可得AD=AB′=AB,证得四边形ABCD是正方形,继而根据题意画出图形,根据翻折的性质以及全等三角形的知识进行推导即可求得答案.
(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴AC=![]() ,
,
∵△APB≌△APB′,
∴∠AB′P=∠B=90°,AB′=AB=2![]() ,BP=B′P,
,BP=B′P,
∴∠B=∠PB′C=90°,B′C=AC-AB′=![]() ,
,
又∵∠PCB′=∠ACB,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴PB′=2![]() -4,
-4,
∴PB=2![]() -4,
-4,
即t=2![]() -4;
-4;
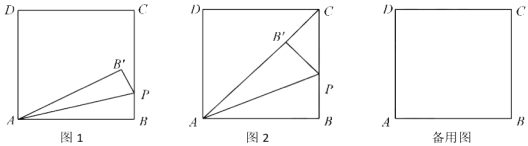
②如图,当∠PCB′=90 °时,此时点B′落在BC上,
在Rt△AB′D中,∠D=90°,∴B′D=![]() ,
,
∴B′C=![]() ,
,
在△PCB′中,由勾股定理得:![]() ,
,
解得t=2;
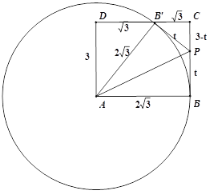
如图,当∠PCB′=90 °时,此时点B′在CD的延长线上,
在Rt△AB′D中,∠ADB′=90°,∴B′D=![]() ,
,
∴B′C=3![]() ,
,
在△PCB′中,由勾股定理得:![]() ,解得t=6;
,解得t=6;
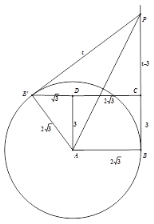
当∠CPB′=90 °时,易得四边形ABPB′为正方形,
∴BP=AB=2![]() ,
,
解得t=2![]() ;
;
综上,t=2或t=6或t=2![]() ;
;
(2)如图
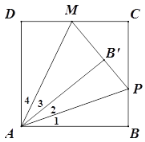
∵∠PAM=45°,
∴∠2+∠3=45°,∠1+∠4=45°,
又∵翻折,
∴∠1=∠2,∠3=∠4,
又∵∠ADM=∠AB′M=90°,AM=AM,
∴△DAM≌△B′AM,
∴AD=AB′=AB,
∴四边形ABCD是正方形,
如图,

设∠APB=x,
∴∠PAB=90°-x,
∴∠DAP=x,
∵AD=AB′,AM=AM,∠ADM=∠AB′M=90°,
∴Rt△MDA≌Rt△B′AM(HL),
∴∠B′AM=∠DAM,
∵翻折,
∴∠PAB=∠PAB′=90°-x,
∴∠DAB′=∠PAB′-∠DAP=90°-2x,
∴∠DAM=![]() ∠DAB′=45°-x,
∠DAB′=45°-x,
∴∠MAP=∠DAM+∠PAD=45°.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知直线![]() ,
,![]() 被直线
被直线![]() 所截,
所截,![]() ,
,![]() 是平面内任意一点(点
是平面内任意一点(点![]() 不在直线
不在直线![]() ,
,![]() ,
,![]() 上),设
上),设![]() ,
,![]() .下列各式:①
.下列各式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,
,![]() 的度数可能是( )
的度数可能是( )

A. ①②③④B. ①②④⑤
C. ①②③⑤D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像的一个交点的横坐标是-3.
的图像的一个交点的横坐标是-3.
(1)求![]() 的值,并在指定坐标系中画出这两个函数的图像;
的值,并在指定坐标系中画出这两个函数的图像;
(2)根据图像,直接写出使一次函数值大于反比例函数值时x的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有单人间、双人间和三人间三种客房供游客租住,某旅行团有18人准备同时租用这三种客房共9间,且每个房间都住满,则租房方案共有______种.
查看答案和解析>>
科目:初中数学 来源: 题型:
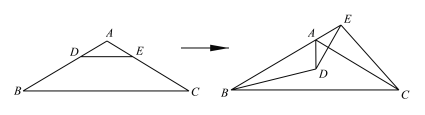
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com