
【题目】如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.

【答案】轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠BAC=30°,
∵C点观测海岛B在北偏东30°方向,∴∠BCD=60°, ∴∠BAC=∠CBA=30°,∴AC=BC.
∵D点观测海岛在北偏西30°方向 ∴∠BDC=60° ∴∠BCD=60° ∴∠CBD=60° ∴△BCD为等边三角形,
∴BC=BD,∵BC=20,∴BC=AC=CD=20,
∵船以每小时10海里的速度从A点航行到C处,又以同样的速度继续航行到D处,
∴船从A点到达C点所用的时间为:20÷10=2(小时),
船从C点到达D点所用的时间为:20÷10=2(小时),
∵船上午11时30分在A处出发,D点观测海岛B在北偏西30°方向,
∴到达D点的时间为13时30分+2小时=15时30分.
答:轮船到达C处的时间为13时30分,到达D处的时间15时30分.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
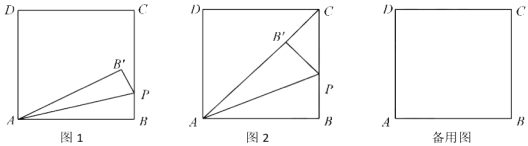
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
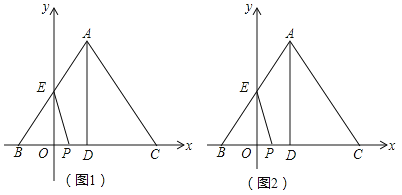
【题目】如图,在平面直角坐标系中, ![]() ,线段
,线段![]() 在轴上,
在轴上, ![]() =12,点
=12,点![]() 的坐标为(-3,0),线段
的坐标为(-3,0),线段![]() 交
交![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,动点
,动点![]() 从原点出发,以每秒3个单位的速度沿
从原点出发,以每秒3个单位的速度沿![]() 轴向右运动,设运动的时间为
轴向右运动,设运动的时间为![]() 秒.
秒.
(1)点![]() 的坐标为(_________),__________);
的坐标为(_________),__________);
(2)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值;
的值;
(3)若点![]() 运动的同时,
运动的同时, ![]() 以
以![]() 为位似中心向右放大,且点
为位似中心向右放大,且点![]() 向右运动的速度为每秒2个单位,
向右运动的速度为每秒2个单位, ![]() 放大的同时高
放大的同时高![]() 也随之放大,当以
也随之放大,当以![]() 为直径的圆与动线段
为直径的圆与动线段![]() 所在直线相切,求
所在直线相切,求![]() 的值和此时C点的坐标.
的值和此时C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( ) 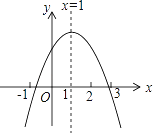
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.

查看答案和解析>>
科目:初中数学 来源: 题型:
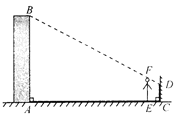
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形纸片ABCD中,AB=4,∠BAD=60°,按如下步骤折叠该菱形纸片:
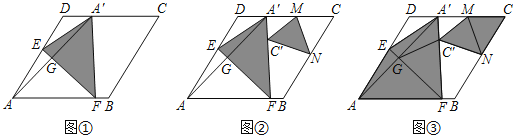
第一步:如图①,将菱形纸片ABCD折叠,使点A的对应点A′恰好落在边CD上,折痕EF分别与边AD、AB交于点E、F,折痕EF与对应点A、A′的连线交于点G.
第二步:如图②,再将四边形纸片BCA′F折叠使点C的对应点C′恰好落在A′F上,折痕MN分别交边CD、BC于点M、N.
第三步:展开菱形纸片ABCD,连接GC′,则GC′最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后探究相关的问题
(阅读)|5﹣2|表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|可以看做|5﹣(﹣2)|,表示5与﹣2的差的绝对值,也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.
(1)如图,先在数轴上画出表示点2.5的相反数的点B,再把点A向左移动1.5个单位,得到点C,则点B和点C表示的数分别为_____和_____,B,C两点间的距离是_____;
(2)数轴上表示x和﹣1的两点A和B之间的距离表示为_____;如果|AB|=3,那么x为_____;
(3)若点A表示的整数为x,则当x为_____时,|x+4|与|x﹣2|的值相等;
(4)要使代数式|x+5|+|x﹣2|取最小值时,相应的x的取值范围是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】代数之父——丢番图(Diophantus)是古希腊的大数学家,是第一位懂得使用符号代表数来研究问题的人. 丢番图的墓志铭与众不同,不是记叙文,而是一道数学题.对其墓志铭的解答激发了许多人学习数学的兴趣,其中一段大意为:他的一生幼年占![]() ,青少年占
,青少年占![]() ,又过了
,又过了![]() 才结婚,5年后生子,子先父4年而卒,寿为其父之半.
才结婚,5年后生子,子先父4年而卒,寿为其父之半.
下面是其墓志铭解答的一种方法:
解:设丢番图的寿命为x岁,根据题意得:
![]() ,
,
解得![]() .
.
∴丢番图的寿命为84岁.
这种解答“墓志铭”体现的思想方法是( )
A.数形结合思想B.方程思想C.转化思想D.类比思想
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com