
【题目】如图所示,已知直线![]() ,
,![]() 被直线
被直线![]() 所截,
所截,![]() ,
,![]() 是平面内任意一点(点
是平面内任意一点(点![]() 不在直线
不在直线![]() ,
,![]() ,
,![]() 上),设
上),设![]() ,
,![]() .下列各式:①
.下列各式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,
,![]() 的度数可能是( )
的度数可能是( )

A. ①②③④B. ①②④⑤
C. ①②③⑤D. ①②③④⑤
【答案】C
【解析】
根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
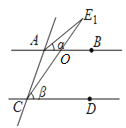
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
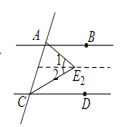
∴∠AE2C=α+β.
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
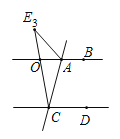
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α-β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
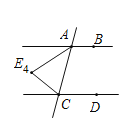
∴∠AE4C=360°-α-β.
∴∠AEC的度数可能为β-α,α+β,α-β,360°-α-β.
(5)(6)当点E在CD的下方时,同理可得,∠AEC=α-β或β-α.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业,如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为![]() ,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,
,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,![]() 于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)
于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的环保建设,提高企业的治污能力某大型企业准备购买A,B两种型号的污水处理设备共8台,若购买A型设备2台,B型设备3台需34万元;购买A型设备4台,B型设备2台需44万元.
(1)求A,B两种型号的污水处理设备的单价各是多少?
(2)已知一台A型设备一个月可处理污水220吨,B型设备一个月可处理污水190吨,若该企业每月处理的污水不低于1700吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B. ![]() C.
C. ![]() D. 30
D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 、点
、点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,
,![]() .射线
.射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.

(1)如图1所示,点![]() 在
在![]() 的延长线上,求
的延长线上,求![]() 的度数.
的度数.
(2)若![]() ,其它条件不变,当点
,其它条件不变,当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() ______;当点
______;当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() ______.(用含
______.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空
已知,如图,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ∥
∥![]()

证明:∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∴_____________=________________
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
∴_____________=________________
∵![]() ∥
∥![]()
∴![]() ___________(两直线平行,内错角相等)
___________(两直线平行,内错角相等)
∴_____________=________________(等量代换)
∴![]() ∥
∥![]() (同位角相等,两直线平行)
(同位角相等,两直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
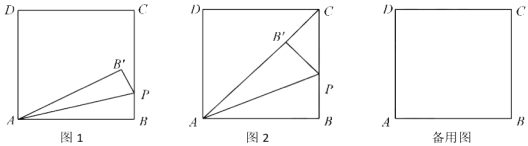
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com