Question

【题目】在中，，，点在边上，点在边上（点、点不与所在线段端点重合），，连接，.射线，延长交射线于点，点在直线上，且.

（1）如图1所示，点在的延长线上，求的度数.

（2）若，其它条件不变，当点在的延长线上时，______；当点在的延长线上时，______.（用含的代数式表示）

Answer 1

【答案】(1)120o;(2)180o-,

【解析】

(1)先证明△ABE≌△ACD得到∠AEB＝∠ADC，再由平行线的性质得到∠A=∠ECM,∠ADC+∠ACD+∠ECM=180o，∠ADC＝∠MCN，综合可得∠EMN＝∠ACD+∠ADC，再根据三角形内角和即可求得;

(2) 当点在的延长线上时，求解方法与（1）相同；当点在的延长线上时，与（1）方法相同先证明∠ACD＝∠EMC，再由可得∠ACD+∠ECM＝∠NME+∠EMC，再代相等的量代入即可得到∠NME＝∠A，即可求得.

（1）∵，，

∴AD＝AE，

在△ABE和△ACD中

，

∴△ABE≌△ACD（SAS），

∴∠AEB＝∠ADC，

又∵∠AEB＝∠MEC(对顶角相等),

∴∠ADC＝∠MEC,

∵CF//AB,∠ADC＝∠MCN，

∴∠A=∠ECM,∠ADC+∠ACD+∠ECM=180o, ∠ADC＝∠MCN，

又∵∠EMC+∠ECM+∠MEC＝180o（三角形内角和为180o）,

∴∠ADC+∠ACD＝∠EMC+∠MEC，

又∵∠ADC＝∠MEC（已证）,

∴∠ACD＝∠EMC，

又∵MN＝CN，

∴∠NCM＝∠NMC，

又∵∠ADC＝∠MCN（已证），

∴∠ADC＝∠NMC，

又∵∠ACD＝∠EMC，∠EMN＝∠ECM+∠NMC，

∴∠EMN＝∠ACD+∠ADC，

在△ACD中，∠ACD+∠ADC+∠A＝180o,

∴∠EMN＝∠ACD+∠ADC=180o-∠A,

又∵∠A＝60o,

∴∠EMN＝180o-60o=120o.即∠BMN＝120o;

(2) 当点在的延长线上时，如图1所示：由（1）得∠EMN＝180o-∠A，

又∵，

∴∠EMN＝180o-,即∠BMN＝180o-；

当点在的延长线上时，如图所示：

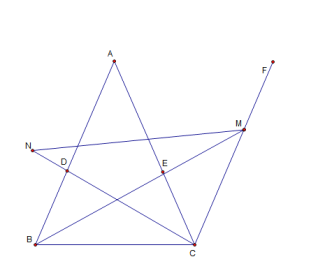
由（1）可得∠ACD＝∠EMC，

∵CF//AB,

∴∠A=∠ECM,

∵NC＝MN，

∴∠NCM＝∠NMC，

又∵∠NCM＝∠ACD+∠ECM，∠NMC＝∠NME+∠EMC，

∴∠ACD+∠ECM＝∠NME+∠EMC，

∴∠ECM＝∠NME，

又∵∠A=∠ECM,

∴∠NME＝∠A，

又∵∠A＝a,

∴∠NME＝a,即∠BMN＝a.