
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
【答案】(1)△BCD是直角三角形(2)P(![]() ,
, ![]() )(3)M(
)(3)M(![]() ,
, ![]() )或M(
)或M(![]() ,
, ![]() )
)
【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式求出b、c的值,然后写出解析式,求得C、D两点的坐标,根据勾股定理及勾股定理的逆定理即可判定△BCD是直角三角形;(2)作PQ⊥OC于点Q,可得△PCQ∽△BDC,根据相似三角形的性质可得PQ=3CQ ,设 设P(3m,-3-m)代入直线BD的解析式求得M的值,即可得点P的坐标;(3)分点M在对称轴右侧和点M在对称轴左侧两种情况进行讨论:(Ⅰ)当点M在对称轴右侧时,分点N在射线CD上和点N在射线DC上两种情况讨论;(Ⅱ)当点M在对称轴左侧时,由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠KCN<45°,所以点M不存在,由此求的M(![]() ,
, ![]() )或M(
)或M(![]() ,
, ![]() ).
).
试题解析:
(1) ![]() ,C(0,-3),D(1,-4)
,C(0,-3),D(1,-4)
∴![]() ,
,
△BCD是直角三角形
(2)作PQ⊥OC于点Q,∴△PCQ∽△BDC,∴PQ=3CQ
设P(3m,-3-m)代入直线BD: ![]() 得:
得:
∴P(![]() ,
, ![]() )
)
(3)M(![]() ,
, ![]() )或M(
)或M(![]() ,
, ![]() )
)


科目:初中数学 来源: 题型:
【题目】某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A. 79.25分 B. 80.75分 C. 81.06分 D. 82.53分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
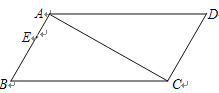
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求![]() 的值;
的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与□ABCD 重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是 ;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、 92、85.
①这组数据的众数是 ,中位数是 ;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
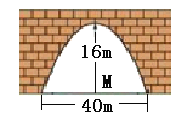
【题目】如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点![]() 的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OM平分∠BOC,ON平分∠AOC, 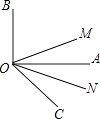
(1)若∠AOB=90°,∠AOC=30°,求∠MON的度数;
(2)若(1)中改成∠AOB=60°,其他条件不变,求∠MON的度数;
(3)若(1)中改成∠AOC=60°,其他条件不变,求∠MON的度数;
(4)从上面结果中看出有什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com