
【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
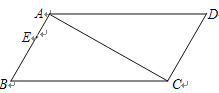
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求![]() 的值;
的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与□ABCD 重叠部分的面积.
【答案】(1)证明见解析(2)![]() =-237(3)
=-237(3)![]()
【解析】试题分析:(1)根据已知条件证得AB∥CD和 AD∥BC,即可判定四边形ABCD是平行四边形;(2)分点P在BC上时和当点P在AD上两种情况求解;(3)设PF与AD交于点M,则△MAP为等腰三角形 , 作MN⊥AP于N,AH⊥BP点H,可得△MPN∽△APH,再根据相似三角形的性质求解即可.
试题解析:
(1)证明:∵∠BAC=∠ACD=90°,
∴AB∥CD,
∵∠B=∠D=60°,∠BAC=∠ACD=90°,
∴∠BCA=∠CAD=30°,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)当点P在BC上时:△BEP为等边三角形,t=2,
∴![]() =-58
=-58
当点P在AD上时:EB=EP,作PH⊥AB,PA=15-t
在Rt△EHP中,由勾股定理得:![]()
∴![]() =-237
=-237
(3)设PF与AD交于点M,则△MAP为等腰三角形
作MN⊥AP于N,AH⊥BP点H,
∴△MPN∽△APH,∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a , b的关系式:①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号)。
学生 | 投进球数 | 没投进球数 | 投进次数 |
甲 | 10 | 5 | 15 |
乙 | a | b | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( ) 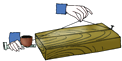
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com