
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
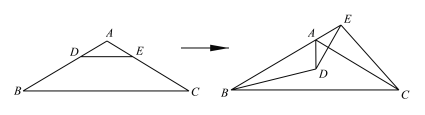
【答案】②③④
【解析】
由AB=AC,∠B=30°,得出∠B=∠C=30°,∠BAC=120°,得出将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,△ADE的旋转角为60°,故①错误;由DE∥BC,易证AD=AE,得出BD=EC,故②正确;BE=AE+AB=AD+AC,故③正确;证明∠DAC=∠EAC,由AD=AE,得出DE⊥AC,故④正确;即可得出结果.
解:∵AB=AC,∠B=30°,
∴∠B=∠C=30°,∠BAC=120°,
∴将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,△ADE的旋转角为180°-120°=60°,故①错误;
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴BD=EC,故②正确;
BE=AE+AB=AD+AC,故③正确;
∵∠BAC=∠DAE=120°,
∴∠EAC=180°-∠BAC=180°-120°=60°,∠DAC=120°-∠EAC=120°-60°=60°,
∴∠DAC=∠EAC,
∵AD=AE,
∴DE⊥AC,故④正确;
故答案为:②③④.


科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)比较大小:![]() +1
+1 ![]() (填“>”、“<”或者“ =”)
(填“>”、“<”或者“ =”)
(2)其实我们可以利用三角形的知识在方格纸上画图验证⑴的结果,请在图①中画出相应的图形(设小正方形的边长为1)

(3)请用(2)中的方法在图②中画图比较大小:![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
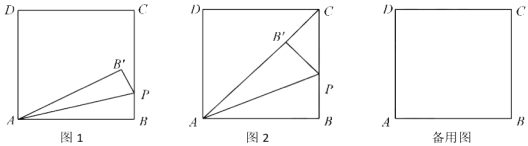
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的三个顶点的坐标分别为A(-3,2)、B(0,4)、C(0,2).
⑴将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C.平移△ABC,若A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
⑵若将△A1B1C绕某一点旋转得到△A2B2C2,请直接写出旋转中心的坐标为 .
⑶在x轴上找一点P,使得直线CP将△ABC的面积分为1:2,直接写出P点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=![]() EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
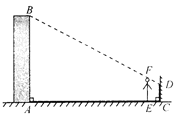
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com