
【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=![]() EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由平行四边形性质和等腰三角形“三线合一”即可得ED⊥CA,根据三角形中位线定理可得EF=![]() AB;由直角三角形斜边上中线等于斜边一半可得EG=
AB;由直角三角形斜边上中线等于斜边一半可得EG=![]() CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得
CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得![]() ;由三角形中位线定理可证得S△OEF=
;由三角形中位线定理可证得S△OEF=![]() S△AOB,进而可得S△EFD=S△OEF+S△ODE=
S△AOB,进而可得S△EFD=S△OEF+S△ODE=![]() SABCD+
SABCD+![]() SABCD=
SABCD=![]() SABCD,再根据E、G分别是OA、CD中点,可得S△CEG=
SABCD,再根据E、G分别是OA、CD中点,可得S△CEG=![]() S△CDE=
S△CDE=![]() SABCD,即可得S△EFD=S△CEG.
SABCD,即可得S△EFD=S△CEG.
解:如图,连接FG,
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD,AD=BC,AD∥BC,AB=CD,AB∥CD
∵BD=2AD
∴OD=AD
∵点E为OA中点
∴ED⊥CA,故①正确;
∵E,F,G分别是OA,OB,CD的中点,
∴EF∥AB,EF=![]() AB,S△OEF=
AB,S△OEF=![]() S△AOB,
S△AOB,
∵∠CED=90°,CG=DG=![]() CD
CD
∴EG=![]() CD
CD
∴EF=EG,故②正确;
∵EF∥CD,EF=DG
∴四边形DEFG是平行四边形
∴EH=HG
即![]() ,故③正确;
,故③正确;
∵S△AOB=S△AOD=![]() SABCD,S△ACD=
SABCD,S△ACD=![]() SABCD,
SABCD,
∴S△OEF=![]() SABCD,
SABCD,
∵AE=OE
∴S△ODE=![]() S△AOD=
S△AOD=![]() SABCD,
SABCD,
∴S△EFD=S△OEF+S△ODE=![]() SABCD+
SABCD+![]() SABCD=
SABCD=![]() SABCD,
SABCD,
∵![]()
∴CE=![]() AC
AC
∴S△CDE=![]() S△ACD=
S△ACD=![]() SABCD,
SABCD,
∵CG=DG
∴S△CEG=![]() S△CDE=
S△CDE=![]() SABCD,
SABCD,
∴S△EFD=S△CEG,故④正确;
故选:D.



科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像的一个交点的横坐标是-3.
的图像的一个交点的横坐标是-3.
(1)求![]() 的值,并在指定坐标系中画出这两个函数的图像;
的值,并在指定坐标系中画出这两个函数的图像;
(2)根据图像,直接写出使一次函数值大于反比例函数值时x的取值范围 .
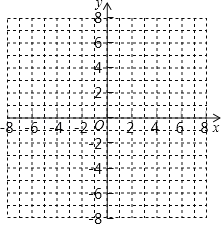
查看答案和解析>>
科目:初中数学 来源: 题型:
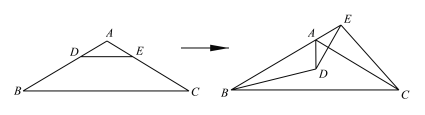
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P、Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
查看答案和解析>>
科目:初中数学 来源: 题型:
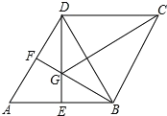
【题目】如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④![]() 其中正确的有______.
其中正确的有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
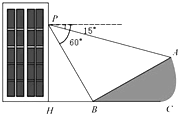
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com