
����Ŀ����֪������y����![]() x2+bx+c������A��4��3��������ΪB���Գ�����ֱ��x��2��
x2+bx+c������A��4��3��������ΪB���Գ�����ֱ��x��2��
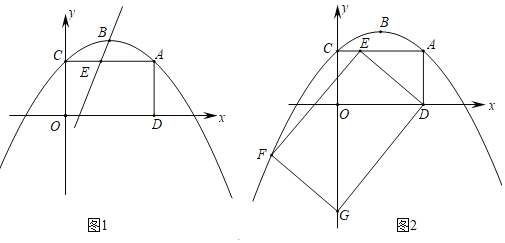
��1���������ߵĺ�������ʽ�Ͷ���B�����ꣻ
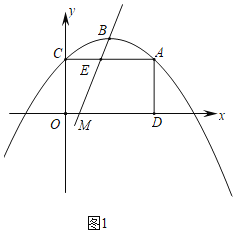
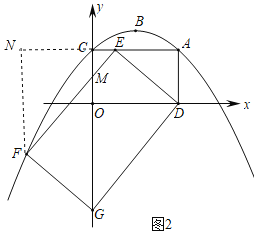
��2����ͼ1����������y�ύ�ڵ�C������AC����A��AD��x���ڵ�D��E���߶�AC�ϵĶ��㣨��E����A��C�����غϣ���
��i����ֱ��BE���ı���ACOD�ֳ������Ϊ1��3�������֣����E�����ꣻ
��ii����ͼ2������DE��������DEFG���ڵ�E���˶������У��Ƿ���ڵ�G����y���ϵ�ͬʱ��Fǡ�������������ϣ������ڣ������ʱAE�ij����������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+x+3������B������Ϊ��2��4������2����i����E������Ϊ��
x2+x+3������B��������2��4������2����i����E��������![]() ��3����
��3����![]() ��3������ii�����ڣ�����G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ
��3������ii�����ڣ�����G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ![]() ��
��
��������
��1��������ó�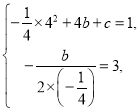 �����
�����![]() ���ó������ߵĺ�������ʽΪ��y����
���ó������ߵĺ�������ʽΪ��y����![]() x2+x+3����
x2+x+3����![]() ��x��2��2+4�����ɵó�����B������Ϊ��2��4����
��x��2��2+4�����ɵó�����B������Ϊ��2��4����
��2����i�����C��0��3�������E������Ϊ��m��3�������ֱ��BE�ĺ�������ʽΪ��y��![]() x+
x+![]() �����M������Ϊ��4m��6��0����������ó�OC��3��AC��4��OM��4m��6��CE��m����S����ACOD��12��S����ECOM��
�����M������Ϊ��4m��6��0����������ó�OC��3��AC��4��OM��4m��6��CE��m����S����ACOD��12��S����ECOM��![]() ��������������m��ֵ���ɣ�
��������������m��ֵ���ɣ�
��ii������F��FN��AC��N����NF��CG�����F����������a����![]() a2+a+3������NF��3������
a2+a+3������NF��3������![]() a2+a+3����
a2+a+3����![]() a2��a��NC����a��֤��EFN�ա�DGO��ASA�����ó�NE��OD��AC��4����AE��NC����a��֤��ENF�ס�DAE���ó�
a2��a��NC����a��֤��EFN�ա�DGO��ASA�����ó�NE��OD��AC��4����AE��NC����a��֤��ENF�ס�DAE���ó�![]() �����a����
�����a����![]() ��0����a��0ʱ����E���A�غϣ���ȥ���ó�AE��NC����a��
��0����a��0ʱ����E���A�غϣ���ȥ���ó�AE��NC����a��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��1����������y����![]() x2+bx+c������A��4��3�����Գ�����ֱ��x��2��
x2+bx+c������A��4��3�����Գ�����ֱ��x��2��
��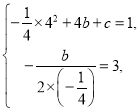
���![]()
�������ߵĺ�������ʽΪ��y����![]() x2+x+3��
x2+x+3��
��y����![]() x2+x+3����
x2+x+3����![]() ��x��2��2+4��
��x��2��2+4��
�ඥ��B������Ϊ��2��4����
��2����i����y����![]() x2+x+3��
x2+x+3��
��x��0ʱ��y��3��
��C���������0��3����
��A��4��3����
��AC��OD��
��AD��x��
���ı���ACOD�Ǿ��Σ�
���E������Ϊ��m��3����ֱ��BE�ĺ�������ʽΪ��y��kx+n��ֱ��BE��x���ڵ�M����ͼ1��ʾ��
��![]()
��ã� 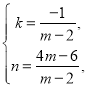 ��
��
��ֱ��BE�ĺ�������ʽΪ��y��![]() x+
x+![]() ��
��
�y��![]() x+
x+![]() ��0����x��4m��6��
��0����x��4m��6��
���M��������4m��6��0����
��ֱ��BE���ı���ACOD�ֳ������Ϊ1��3�������֣�
���M���߶�OD�ϣ���M�����O�غϣ�
��C��0��3����A��4��3����M��4m��6��0����E��m��3����
��OC��3��AC��4��OM��4m��6��CE��m��
��S����ACOD��OCAC��3��4��12��
S����ECOM��![]() ��OM+EC��OC��
��OM+EC��OC��![]() ��4m��6+m����3��
��4m��6+m����3��![]() ��
��
�����������
��![]() ��
��![]() ����
����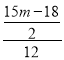 ��
��![]() ��
��
��ã�m��![]() ��
��
���E����������![]() ��3����
��3����
��![]() ��
��![]() ����
����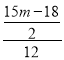 ��
��![]() ��
��
��ã�m��![]() ��
��
���E����������![]() ��3����
��3����
������������E����������![]() ��3����
��3����![]() ��3����
��3����
��ii�����ڵ�G����y���ϵ�ͬʱ��Fǡ�������������ϣ��������£�
������ã����������ľ���DEFG��ֱ��AC���·���
����F��FN��AC��N����NF��CG����ͼ2��ʾ��
���F����������a����![]() a2+a+3����
a2+a+3����
��NF��3������![]() a2+a+3����
a2+a+3����![]() a2��a��NC����a��
a2��a��NC����a��
���ı���DEFG���ı���ACOD���Ǿ��Σ�
���DAE����DEF����N��90�㣬EF��DG��EF��DG��AC��OD��
���NEF����ODG����EMC����DGO��
��NF��CG��
���EMC����EFN��
���EFN����DGO��
�ڡ�EFN�͡�DGO�У���NEF=��ODG��EF=DG,��EFN=��DGO��
���EFN�ա�DGO��ASA����
��NE��/span>OD��AC��4��
��AC��CE��NE��CE����AE��NC����a��
�ߡ�DAE����DEF����N��90�㣬
���NEF+��EFN��90�㣬��NEF+��DEA��90�㣬
���EFN����DEA��
���ENF�ס�DAE��
��![]() ����
����![]() ��
��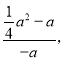
�����ã�![]() a2+a��0��
a2+a��0��
��ã�a����![]() ��0��
��0��
��a��0ʱ����E���A�غϣ�
��a��0��ȥ��
��AE��NC����a��![]() ��
��
�൱��G����y���ϵ�ͬʱ��Fǡ�������������ϣ���ʱAE�ij�Ϊ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����
x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����

��1���������ߵĽ���ʽ������D�����ꣻ
��2���ж���ABC����״��֤����Ľ��ۣ�
��3����M��x���ϵ�һ�����㣬����DCM���ܳ���Сʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0���Ķ�������A����1��3������x���һ������B����4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ���2a��b=0����abc��0������������x�����һ�����������ǣ�3��0�����ܷ���ax2+bx+c��3=0��������ȵ�ʵ�������ݵ���4��x����1ʱ����y2��y1��
������ȷ���ǣ�������

A. �٢ڢ� B. �٢ۢ� C. �٢ܢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C�ǰ�ԲO��һ�㣨�����A��B�غϣ���D��![]() ���е㣬DE��AB�ڵ�E������C����ԲO�����ߣ���ED���ӳ����ڵ�F��
���е㣬DE��AB�ڵ�E������C����ԲO�����ߣ���ED���ӳ����ڵ�F��
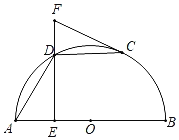
��1����֤����FCD����ADE��
��2����գ�
�ٵ���FCD�Ķ���Ϊ�� ��ʱ���ı���OADC�����Σ�
����AB��2![]() ����CF��ABʱ��DF�ij�Ϊ�� ����
����CF��ABʱ��DF�ij�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x3��ax2��2ax+a2��1��0ֻ��һ��ʵ��������a��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
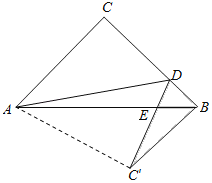
����Ŀ����ͼ���ڡ�ABC�У�AC��BC��4����C��90����D��BC����һ�㣬��CD��3BD������AD���ѡ�ACD��AD���ۣ��õ���ADC'��DC����AB���ڵ�E������BC�������BDC'�����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5G���磬������һ�������ƶ�ͨ�ż����������ݴ�������Զ������ǰ�ķ������磬��߿ɴ�10Gbit/s����4G��100����5G�ֻ�Ҳ��Ϊ�����������ȱ�ٵ��ƶ��豸��ij���̹�˾��������5G�ֻ�����֪�۳�5��A���ֻ���3��B���ֻ������۶�Ϊ51000Ԫ���۳�3��A���ֻ���2��B���ֻ������۶�Ϊ31500Ԫ��
��1����A���ֻ���B���ֻ����ۼ۷ֱ��Ƕ���Ԫ��
��2���õ��̹�˾��3��ʵ����������������������Ϊ�������ֻ���3000Ԫ��500Ԫ����5000Ԫ��1500Ԫ��ÿ���ֻ�ֻ�ܲμ����������������3��A���ֻ���������B���ֻ���![]() ��4�¸õ��̹�˾�Ӵ��������ȣ�ÿ��A���ֻ�����3����������ۼ��ٽ�
��4�¸õ��̹�˾�Ӵ��������ȣ�ÿ��A���ֻ�����3����������ۼ��ٽ�![]() a%��������3������2a%��ÿ��B���ֻ�������������ۼ��ٽ�a%��������3����������
a%��������3������2a%��ÿ��B���ֻ�������������ۼ��ٽ�a%��������3����������![]() a%�����4�µ������ܶ��3�µ������ܶ��
a%�����4�µ������ܶ��3�µ������ܶ��![]() a%����a��ֵ��
a%����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����г�����ij���������������ǰϦ������һ��Ʒ���±���ÿ�н�����40Ԫ�����й涨ÿ���ۼ۲�������45Ԫ�������������۾��鷢�֣����ۼ۶�Ϊÿ��45Ԫʱ��ÿ���������700�У�ÿ���ۼ�ÿ���1Ԫ��ÿ��Ҫ������20�У�
��1����д��ÿ�����������![]() ��Ԫ����ÿ���Ǽ�
��Ԫ����ÿ���Ǽ�![]() ��Ԫ��֮��ĺ�����ϵʽ���Ա���
��Ԫ��֮��ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ���Ǽ�Ϊ����Ԫʱ��ÿ�����������![]() �����������Ƕ��٣�
�����������Ƕ��٣�
��3�����������Ҫÿ���ò�����6000Ԫ��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��6��BC��3����E���߶�BA�ϴ�B����ÿ��1����λ���ٶȳ�����A���˶���F������CD��һ���㣬�ڵ�E��F�˶��Ĺ�����ʼ�ձ���EF��5����CF>BE����P��EF���е㣬����AP�����E�˶�ʱ��Ϊts��



��1���ڵ�E��F�˶��Ĺ�������AP�ij��ȴ���һ����Сֵ����AP�ij���ȡ����Сֵʱ����P��λ��Ӧ���� ��
��2����AP��EFʱ�������ʱt��ֵ
��3����PΪԲ������P������P�����ABCD��������ֱ�߶�����ʱ�������ʱt��ֵ����ָ����ʱ��P�İ뾶����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com