
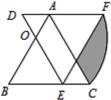
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
【答案】![]()
【解析】
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.根据三线合一求出BG= AG=3,进而求得OG,由三角函数求得CG,解直角三角形OGC得出OC长,再由面积公式分别求得![]() ,
,![]() =
=![]() ,
,![]() ,
,![]() ,利用
,利用![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() 求得答案即可.
求得答案即可.
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.
∵BO=2AO=4,
∴AO=2,AB=6,
∵△ABC为等边三角形,CG⊥AB,
∴BG= AG=![]() AB=3,CG=BC·sin60°=
AB=3,CG=BC·sin60°= ![]() ,
,
∴OG=3-2=1,
Rt△OGC中,OG=1,CG=![]() ,
,
∴OC=![]() =
=![]() ,
,
易证△NEC,△AOD,△BOE为等边三角形,四边形AOEF为等腰梯形,
∴AF=OE=4,CE=AO=2,OM=HF=4×sin60°=![]() ,
,

∵′![]() =
=  =
= ![]() ,
, ![]() =
=![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线![]() 的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线![]() 于点H,连结OP,试求△OPH的面积;
于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线![]() 的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.
(1)求一根跳绳和一个毽子的售价分别是多少元;
(2)学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)

(1)求A,B两品牌足球的单价各为多少元;
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进人积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
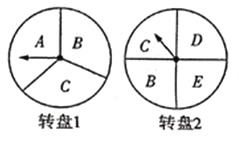
(1)用树状图或列表的方法表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
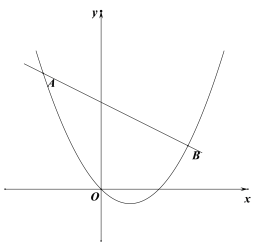
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式.
(2)在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,求
,求![]() 的面积等于20.
的面积等于20.
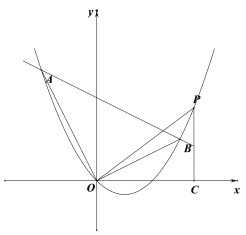
(3)若![]() 在抛物线上,作
在抛物线上,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
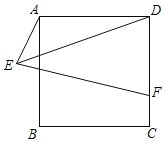
【题目】如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则2EF+ED的最小值为( )
A.12![]() B.12
B.12![]() C.12D.10
C.12D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com