
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线![]() 的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线![]() 于点H,连结OP,试求△OPH的面积;
于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线![]() 的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)![]() (2)①
(2)①![]() ②存在满足条件的点P,点P坐标为:(7﹣4
②存在满足条件的点P,点P坐标为:(7﹣4![]() ,4)
,4)
【解析】
试题(1)利用待定系数法求出抛物线的解析式;(2)①如答图1,作辅助线,利用关系式S△OPH=S△OMH-S△OMP求解;②本问涉及复杂的分类讨论,如答图2所示.由于点P可能在OC、BC、BK、AK、OA上,而等腰三角形本身又有三种情形,故讨论与计算的过程比较复杂,需要耐心细致、考虑全面.
试题解析:(1)由题意得:A(4,0),C(0,4),对称轴为x=1.
设抛物线的解析式为y=ax2+bx+c,则有:
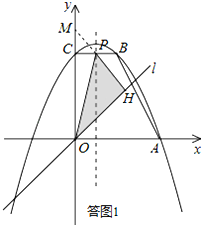
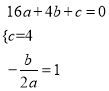 , 解得
, 解得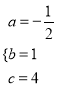 .
.
∴抛物线的函数解析式为:![]()
(2)①当m=0时,直线![]() :y=x.
:y=x.
∵抛物线对称轴为x=1,
∴CP=1.
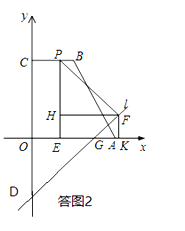
如答图1,延长HP交y轴于点M,则△OMH、△CMP均为等腰直角三角形.
∴CM=CP=1,
∴OM=OC+CM=5.
S△OPH=S△OMH﹣S△OMP=![]() (
(![]() OM)2﹣
OM)2﹣![]() OMCP=
OMCP=![]() ×(
×(![]() ×5)2﹣
×5)2﹣![]() ×5×1=
×5×1=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△OPH=![]() .
.
②当m=﹣3时,直线l:y=x﹣3.
设直线![]() 与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).
与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).
假设存在满足条件的点P.如答图2所示,此时PE=4.
若PE=PF,则点P为∠OGD的角平分线与BC的交点,有GE=GF,过点F分别作FH⊥PE于点H,FK⊥x轴于点K,
∵∠OGD=135°,
∴∠EPF=45°,即△PHF为等腰直角三角形,
设GE=GF=t,则GK=FK=EH=![]() t,
t,
∴PH=HF=EK=EG+GK=t+![]() t,
t,
∴PE=PH+EH=t+![]() t+
t+![]() t=4,
t=4,
解得t=4![]() ﹣4,则OE=3﹣t=7﹣4
﹣4,则OE=3﹣t=7﹣4![]() ,
,
∴P2(7﹣4![]() ,4)
,4)
另外,PE=EF,EF=PF不可能.
综上所述,存在满足条件的点P,点P坐标为:(7﹣4![]() ,4).
,4).

综上所述,存在满足条件的点P,点P坐标为:(7﹣4![]() ,4)
,4)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(发现证明)
如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.

小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.
(2)(类比引申)①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).

(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
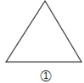
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
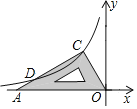
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=-![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
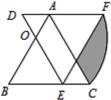
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络,是最新一代蜂窝移动通信技术,其数据传输速率远高于以前的蜂窝网络,最高可达10Gbit/s,比4G快100倍.5G手机也成为生活、工作不可缺少的移动设备,某电商公司销售两种5G手机,已知售出5部A型手机,3部B型手机的销售额为51000元;售出3部A型手机,2部B型手机的销售额为31500元.
(1)求A型手机和B型手机的售价分别是多少元;
(2)该电商公司在3月实行“满减促销”活动,活动方案为:单部手机满3000元减500元,满5000元减1500元(每部手机只能参加最高满减活动),结果3月A型手机的销量是B型手机的![]() ,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降
,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降![]() a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加
a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加![]() a%,结果4月的销售总额比3月的销售总额多
a%,结果4月的销售总额比3月的销售总额多![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com