
【题目】(1)(发现证明)
如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.

小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.
(2)(类比引申)①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3![]() ,求AF的长.
,求AF的长.
【答案】(1)证明见解析;(2)①不成立,结论:EF=DF﹣BE;证明见解析;②BE=EF+DF;(3)AF=![]() .
.
【解析】
(1)【发现证明】
证明△EAF≌△GAF,可得出EF=FG,则结论得证;
(2)【类比引申】
①将△ABE绕点A顺时针旋转90°至△ADM根据SAS可证明△EAF≌△MAF,可得EF=FM,则结论得证;
②将△ADF绕点A逆时针旋转90°至△ABN,证明△AFE≌△ANE,可得出EF=EN,则结论得证;
(3)【联想拓展】
求出DG=2,设DF=x,则EF=DG=x+3,CF=6﹣x,在Rt△EFC中,得出关于x的方程,解出x则可得解.
(1)【发现证明】
证明:把△ABE绕点A顺时针旋转90°至△ADG,如图1,
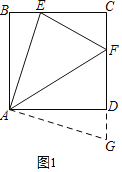
∴∠BAE=∠DAG,AE=AG,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠DAG+∠FAD=45°,
∴∠EAF=∠FAG,
∵AF=AF,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=DF+BE;
(2)【类比引申】
①不成立,结论:EF=DF﹣BE;
证明:如图2,将△ABE绕点A顺时针旋转90°至△ADM,
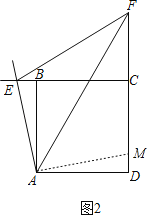
∴∠EAB=∠MAD,AE=AM,∠EAM=90°,BE=DM,
∴∠FAM=45°=∠EAF,
∵AF=AF,
∴△EAF≌△MAF(SAS),
∴EF=FM=DF﹣DM=DF﹣BE;
②如图3,将△ADF绕点A逆时针旋转90°至△ABN,
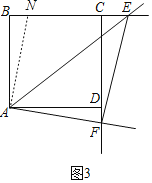
∴AN=AF,∠NAF=90°,
∵∠EAF=45°,
∴∠NAE=45°,
∴∠NAE=∠FAE,
∵AE=AE,
∴△AFE≌△ANE(SAS),
∴EF=EN,
∴BE=BN+NE=DF+EF.
即BE=EF+DF.
故答案为:BE=EF+DF.
(3)【联想拓展】
解:由(1)可知AE=AG=3![]() ,
,
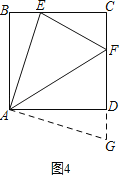
∵正方形ABCD的边长为6,
∴DC=BC=AD=6,
∴![]() =
=![]() =3.
=3.
∴BE=DG=3,
∴CE=BC﹣BE=6﹣3=3,
设DF=x,则EF=DG=x+3,CF=6﹣x,
在Rt△EFC中,∵CF2+CE2=EF2,
∴(6﹣x)2+32=(x+3)2,
解得:x=2.
∴DF=2,
∴AF=![]() =
=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月24日《复仇者联盟4》在中国大陆上映.我市江北UME影城为加大宣传,决定在4月23日预售普通3D票400张和IMAX票100张,且预售中的IMAX的票价是普通3D票价的2倍.
(1)若影城的预售总额不低于21000元,则普通3D票的预售价格最少为多少元?
(2)影城计划在上映当天推出普通3D票3200张,IMAX票800张.由于预售的火爆,影城决定将普通3D票的价格在(1)中最低价格的基础上增加![]() %,而IMAX票价在(1)中IMAX票价上增加了a元,结果普通3D票的销售量比计划少2a%.IMAX票的销售量与计划保持一致,最终实际销售额与计划销售额相等,求a的值.
%,而IMAX票价在(1)中IMAX票价上增加了a元,结果普通3D票的销售量比计划少2a%.IMAX票的销售量与计划保持一致,最终实际销售额与计划销售额相等,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1的坐标为(2,4),以点O为圆心,以OA1长为半径画弧,交直线y=x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线y=x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线y=x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线y=x于点B4,…按照如此规律进行下去,点B2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线![]() 的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线![]() 于点H,连结OP,试求△OPH的面积;
于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线![]() 的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
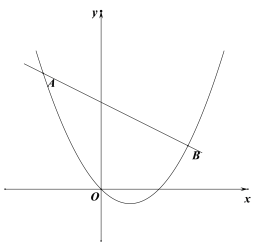
(1)求抛物线的解析式.
(2)在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,求
,求![]() 的面积等于20.
的面积等于20.
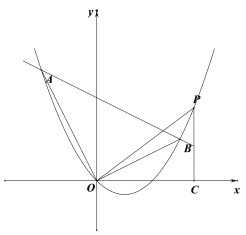
(3)若![]() 在抛物线上,作
在抛物线上,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com