【题目】校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道
上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=300，∠CBD=600．
(1)求AB的长(精确到0.1米，参考数据：
)；
(2)已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由．
科目：初中数学 来源： 题型：
【题目】如图，某高楼OB上有一旗杆CB，我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度，由于有其他建筑物遮挡视线不便测量，所以测量员沿坡度i=1：
的山坡从坡脚的A处前行50米到达P处，测得旗杆顶部C的仰角为45°，旗杆底部B的仰角为37°（测量员的身高忽略不计），已知旗杆高BC=15米，则该高楼OB的高度为（ ）米．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A. 45 B. 60 C. 70 D. 85
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在直角坐标系xOy中，A（3，4），B（1，2），C（5，1）．
（1）作出△ABC关于y轴的对称图形△A1B1C1；
（2）写出△A1B1C1的顶点坐标；
（3）求出△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】大润发超市在销售某种进货价为20元/件的商品时，以30元/件售出，每天能售出100件．调查表明：这种商品的售价每上涨1元/件，其销售量就将减少2件．
（1）为了实现每天1600元的销售利润，超市应将这种商品的售价定为多少？
（2）设每件商品的售价为x元，超市所获利润为y元．
①求y与x之间的函数关系式；
②物价局规定该商品的售价不能超过40元/件，超市为了获得最大的利润，应将该商品售价定为多少？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图1，直线
与x轴、y轴分别交于点A、C两点，点B的横坐标为2．
图1 图2
（1）求A、C两点的坐标和抛物线的函数关系式；
（2）点D是直线AC上方抛物线上任意一点，P为线段AC上一点，且S△PCD＝2S△PAD ，求点P的坐标；
（3）如图2，另有一条直线y＝－x与直线AC交于点M，N为线段OA上一点，∠AMN＝∠AOM．点Q为x轴负半轴上一点，且点Q到直线MN和直线MO的距离相等，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
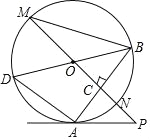
【题目】如图，已知⊙O中，AB为弦，直线PO交⊙O于点M、N，PO⊥AB于C，过点B作直径BD，连接AD、BM、AP．
（1）求证：PM∥AD；
（2）若∠BAP=2∠M，求证：PA是⊙O的切线；
（3）若AD=6，tan∠M=
，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋．甲、乙两种绿色袋装食品的进价和售价如表．已知：用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同．
甲 | 乙 | |
进价（元/袋） | m | m﹣2 |
售价（元/袋） | 20 | 13 |
（1）求m的值；
（2）假如购进的甲、乙两种绿色袋装食品全部卖出，所获总利润不少于5200元，且不超过5280元，问该超市有几种进货方案？（利润＝售价﹣进价）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中,
(1) 取点M(1，0)，则点M到直线l： 
的距离为_________，取直线
与直线l平行，则两直线距离为_________.
(2) 已知点P为抛物线y＝x2－4x的x轴上方一点，且点P到直线l： 
的距离为
，求点P的坐标.
(3) 若直线y＝kx＋m与抛物线y＝x2－4x相交于x轴上方两点A、B（A在B的左边），且∠AOB＝90°，求点P(2，0)到直线y＝kx＋m的距离的最大时直线y＝kx＋m的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，∠A′B′C′可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（ ）
A. 4
B. 6 C. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
