
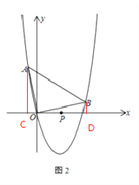
【题目】在平面直角坐标系中,
(1) 取点M(1,0),则点M到直线l: ![]() 的距离为_________,取直线
的距离为_________,取直线![]() 与直线l平行,则两直线距离为_________.
与直线l平行,则两直线距离为_________.
(2) 已知点P为抛物线y=x2-4x的x轴上方一点,且点P到直线l: ![]() 的距离为
的距离为![]() ,求点P的坐标.
,求点P的坐标.
(3) 若直线y=kx+m与抛物线y=x2-4x相交于x轴上方两点A、B(A在B的左边),且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离的最大时直线y=kx+m的解析式.


【答案】(1) ![]() ,
, ![]() ;(2) P(
;(2) P(![]() ,
, ![]() );(3) y=-2x+9.
);(3) y=-2x+9.
【解析】试题分析:(1) 利用直线的正切值即可.(2) 先求出直线与坐标轴的交点坐标,过点E作EG⊥EF交y轴于G,根据已知条件求出EG=![]() ,过点G并且和直线平行的另一条直线就可以画出,根据平行线的性质,求出解析式,联立抛物线解析式即可求出点P的坐标.(3)本题设A(x1,x12-4x)、B(x2,x22-4x),利用一线三等角,得到相似三角形,得AC·BD=OC·OD,求出两根的关系是,再联立方程组,求出直线经过的定点,从而确定距离最远的位置,求出解析式即可.
,过点G并且和直线平行的另一条直线就可以画出,根据平行线的性质,求出解析式,联立抛物线解析式即可求出点P的坐标.(3)本题设A(x1,x12-4x)、B(x2,x22-4x),利用一线三等角,得到相似三角形,得AC·BD=OC·OD,求出两根的关系是,再联立方程组,求出直线经过的定点,从而确定距离最远的位置,求出解析式即可.
试题解析:
解:(1) ![]() ,
, ![]() (利用直线的tan值)
(利用直线的tan值)
(2) 设直线l:y=![]() x-1与x轴、y轴相交于点E、F
x-1与x轴、y轴相交于点E、F
∴E(2,0)、F(0,-1)
过点E作EG⊥EF交y轴于G
∴tan∠EGF=![]()
∴OG=4
∴GE=![]()
∴过点G作直线l的平行线交抛物线于点P,则点P即为所求的点
设直线PG的解析式为![]()
由x2-4x=![]() ,解得
,解得![]()
∴P(![]() ,
, ![]() )
)

(3) 设A(x1,x12-4x)、B(x2,x22-4x)
过点A作AC⊥x轴于C,过点B作BD⊥x轴于D
∴Rt△AOC∽Rt△OBD
∴AC·BD=OC·OD
∴(x12-4x1)(x22-4x2)=-x1x2,x1x2-4(x1+x2)+17=0
联立![]() ,整理得x2-(k+4)x-m=0
,整理得x2-(k+4)x-m=0
∴x1+x2=k+4,x1x2=-m
∴-m-4(k+4)+17=0,m=1-4k
∴直线的解析式为y=kx-4k+1,必过定点Q(4,1)
当点P(2,0)到直线y=kx+m的距离最大时,PQ⊥AB
此时直线的解析式为y=-2x+9.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】(本题10分)对于平面直角坐标系xOy中的点P(a,b),若点P的坐标为(a+![]() ,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+
,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+![]() ,2×1+4),即P′(3,6).
,2×1+4),即P′(3,6).
(1) ① 点P(-1,-2)的“2属派生点”P′的坐标为_______________
② 若点P的“k属派生点”为P′(3,3),请写出一个符合条件的点P的坐标_____________
(2) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且△OPP′为等腰直角三角形,则k的值为____________
(3) 如图,点Q的坐标为(0, ![]() ),点A在函数
),点A在函数![]() (x<0)的图象上,且点A是点B的“
(x<0)的图象上,且点A是点B的“![]() 属派生点”.当线段BQ最短时,求B点坐标.
属派生点”.当线段BQ最短时,求B点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判别四边形是平行四边形的是 ( )
A. 一组对边相等,另一组对边平行 B. 一组对边平行,一组对角互补
C. 一组对角相等,一组邻角互补 D. 一组对角互补,另一组对角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H. 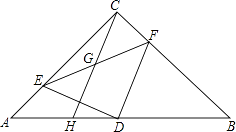
(1)若E在边AC上. ①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com