
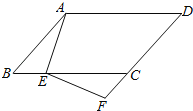
【题目】如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由平行四边形的性质可知AB∥CD,AD∥BC.所以∠B=∠ECF,∠DAE=∠AEB,又因为又∠DAE=∠F,进而可证明△ABE∽△ECF;
(2)由(1)可知:△ABE∽△ECF,得出![]() =
=![]() ,由平行四边形的性质可知BC=AD=8,所以EC=BC﹣BE=8﹣2=6,代入计算求出CF,即可得出答案.
,由平行四边形的性质可知BC=AD=8,所以EC=BC﹣BE=8﹣2=6,代入计算求出CF,即可得出答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,CD=AB,
∴∠B=∠ECF,∠DAE=∠AEB.
又∵∠DAE=∠F,
∴∠AEB=∠F.
∴△ABE∽△ECF;
(2)解:∵△ABE∽△ECF,
![]()
![]()
∵四边形ABCD是平行四边形,
∴BC=AD=8.CD=AB=5,
∴EC=BC﹣BE=8﹣2=6.
∴![]()
∴CF=![]() ,
,
∴FD=CD+CF=![]()


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
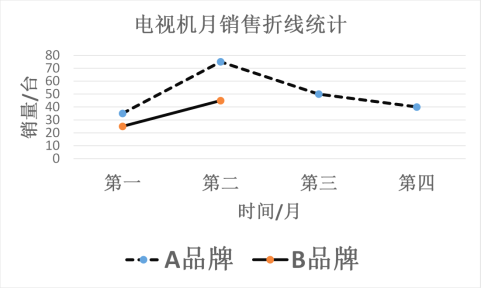
【题目】某商店在四个月的试销期内,只销售A,B两个品牌的电视机,共售出400台.试销结束后,将决定经销其中的一个品牌,为作出决定,经销人员正在绘制两幅统计图,如图
(1)第四个月销量占总销量的百分比是_______;
(2)在图中补全表示B品牌电视机月销量的折线;
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,求抽到B品牌电视机的概率;
(4)经计算,两个品牌电视机月销量的平均水平相同,请你结合折线的走势进行简要分析,判断该商店应经销哪个品牌的电视机.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax﹣3a(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=OC,直线y=﹣x与该抛物线交于E,F两点.
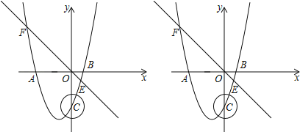
(1)求抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
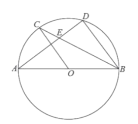
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数
的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数![]() 的图像与y轴相交于点D,其中
的图像与y轴相交于点D,其中![]() .
.
(1)分别求出A、B、C三点的坐标(可以用含有字母a的代数式表示).
(2)点P与点C关于抛物线的对称轴成轴对称,点Q为抛物线上的一个动点.
①试说明点P在直线![]() 的图像上.
的图像上.
②若点Q在抛物线上有且只有三个位置满足![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读新知
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个非零常数,这个数列就叫做等比数列.这个常数叫做等比数列的公比,公比通常用字母![]() 表示(
表示(![]() ).
).
即:在数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() .(
.(![]() 为正整数)中,若
为正整数)中,若![]() ,
,![]() ,…,则数列
,…,则数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() .(
.(![]() 为正整数)叫做等比数列.其中
为正整数)叫做等比数列.其中![]() 叫数列的首项,
叫数列的首项,![]() 叫第二项,…,
叫第二项,…,![]() 叫第
叫第![]() 项,
项,![]() 叫做数列的公比.
叫做数列的公比.
例如:数列1,2,4,8,16,…是等比数列,公比![]() .
.
计算:求等比数列1,3,![]() ,
,![]() ,…,
,…,![]() 的和.
的和.
解:令![]() ,则
,则![]() .
.
因此![]() .所以
.所以![]() .
.
即![]() .
.
学以致用
(1)选择题:下列数列属于等比数列的是( )
A.1,2,3,4,5 B.2,6,18,21,63
C.56,28,14,7,![]() D.-11,22,-33,44,-55
D.-11,22,-33,44,-55
(2)填空题:已知数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是公比为4的等比数列,若它的首项
是公比为4的等比数列,若它的首项![]() ,则它的第
,则它的第![]() 项
项![]() 等于_________.
等于_________.
(3)解答题:求等比数列1,5,![]() ,
,![]() ,…前2021项的和.
,…前2021项的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
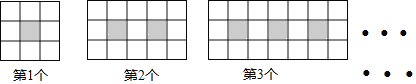
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
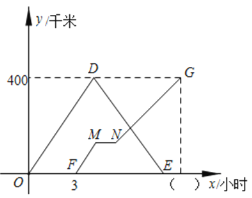
【题目】甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com