
【题目】如图,抛物线y=ax2+2ax﹣3a(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=OC,直线y=﹣x与该抛物线交于E,F两点.
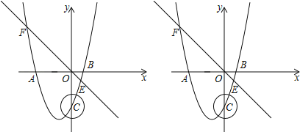
(1)求抛物线的解析式.
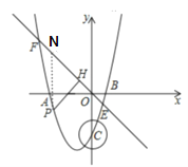
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3;(2)![]() ;(3)点D的坐标为(
;(3)点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(1,﹣3)或(
)或(1,﹣3)或(![]() ,
,![]() ).
).
【解析】
(1)令x=0,则y=﹣3a,可知点C(0,﹣3a),继而知点A的坐标,根据抛物线y=ax2+2ax﹣3a(a≠0)与x轴交于A、B两点可知,ax2+2ax﹣3a=0,解方程可得点A、B的坐标,继而求出a的值及抛物线解析式;
(2)过点P作PM⊥y轴交直线EF于点M,设点P![]() ,点M
,点M![]() ,则PH=
,则PH=![]() =
=![]() ,将表达式配成顶点式即可得出答案;
,将表达式配成顶点式即可得出答案;
(3)分∠BCD=90°、∠CDB=90°两种情况,作出图形分别求解即可.
(1)令x=0,则y=﹣3a,可知点C(0,﹣3a),
∵OA=OC
∴点A(﹣3a,0),
令![]() ,即
,即![]()
解得:x1=﹣3,x2=1
∴点A(﹣3,0),B(1,0)
∴﹣3a=﹣3
∴a=1
∴抛物线的解析式y=x2+2x﹣3
(2)过点P作PN⊥y轴交直线EF于点N,
∵直线EF的解析式为y=﹣x,
∴∠NOA=45°,
∴∠PNH=45°
设点P![]() ,点N
,点N![]() ,
,
∴PH=![]() =
=![]() =
=![]() ,
,
当x=![]() 时,PH的值最大为
时,PH的值最大为![]() ,
,
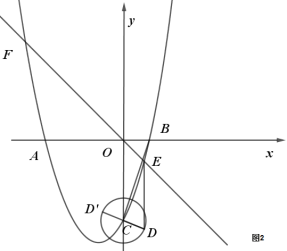
(3)当∠BCD=90°时,如图2左侧图所示,
当点D在BC的右侧时,
过点D作DM⊥y轴于点M,则CD=OB=1,OC=3,
tan∠BCO=![]() =tan∠CDM=
=tan∠CDM=![]() ,
,
则![]() ,
,![]() ,
,
∴xD=CD![]() =
=![]() ,同理yD=
,同理yD=![]() ,
,
故点D(![]() ,
,![]() );
);
同理当点D在BC的左侧时,点D的坐标(![]() ,
,![]() );
);
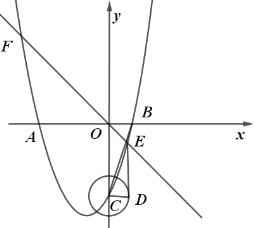
当∠CDB=90°时,如图2右侧图所示,
当点D在BC的右侧时,
CD=OB=1,则点D(1,﹣3),
当点D在BC的左侧时,由点的对称性,同理可得:点D(![]() ,
,![]() );
);
综上所述,点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(1,﹣3)或(
)或(1,﹣3)或(![]() ,
,![]() ).
).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】为全面推进“三供一业”分离移交工作,甲、乙两个工程队承揽了某社区2400米的电路管道铺设工程.已知甲队每天铺设管道的长度是乙队每天铺设管道长度的1.5倍,若两队各自独立完成1200米的铺设任务,则甲队比乙队少用10天.
(1)求甲、乙两工程队每天分别铺设电路管道多少米;
(2)若甲队参与该项工程的施工时间不得超过20天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=5cm,点C是半圆O上的动点,连结AC、BC.设AC=x(单位:cm),△ABC的面积为y(单位:cm2,当点C与A、B重合时,y的值为0).轩轩根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是轩轩的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了x与y的几组值,结果如表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y/cm2 | 0 | 1.25 | 2.45 | 3.58 | 4.57 | 5.41 | 6.25 | 4.91 | 0 |
该函数的表达式为__________,自变量x的取值范围为___________.
(2)在右图中建立平面直角坐标系,描出以补全后的表中各组对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:在(2)问的直角坐标系中画出直线y1=x,根据图象得出当y=y1时x的正数值约为_______(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
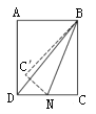
【题目】如图,在矩形ABCD中,AB=3,BC=4,点N为边DC上一动点(不与C、D重合),连接BN,作C关于直线BN的对称点C′连接B C′, C′N,当C′恰好在△ABD的边上时,CN的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
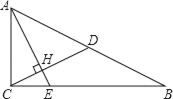
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
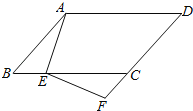
【题目】如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
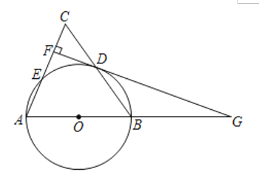
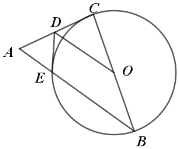
【题目】如图,已知在![]() 中,
中,![]() ,以BC为直径作
,以BC为直径作![]() 交
交![]() 于点
于点![]() ,
,![]() 为AC边的中点,连接
为AC边的中点,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)①若AC=3,AE=1,求![]() 的半径;
的半径;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com