
【题目】如图,已知在![]() 中,
中,![]() ,以BC为直径作
,以BC为直径作![]() 交
交![]() 于点
于点![]() ,
,![]() 为AC边的中点,连接
为AC边的中点,连接![]() .
.
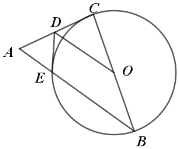
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)①若AC=3,AE=1,求![]() 的半径;
的半径;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
【答案】(1)详见解析;(2)①![]() ②
②![]()
【解析】
(1)连接OE、CE,由圆周角定理得出∠BEC=90°,则∠AEC=90°,由直角三角形斜边上的中线性质得出AD=CD=DE,由等腰三角形的性质得出∠DEC=∠DCE,∠OCE=∠OEC,证出∠OED=90°,即可得出结论;
(2)①由勾股定理求出CE=2![]() ,证△OCE∽△DAE,得出比例式,求出OC的长即可;
,证△OCE∽△DAE,得出比例式,求出OC的长即可;
②证△ABC是等腰直角三角形,得出∠ABC=45°,证四边形OCDE是矩形,由OC=OE,即可得出四边形OCDE是正方形.
(1)证明:连接OE、CE,如图所示:
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠AEC=90°,
∵D是AC的中点,
∴DE=![]() AC=AD=CD,
AC=AD=CD,
∴∠DEC=∠DCE,
∵OC=OE,
∴∠OCE=∠OEC,
∵∠ACB=90°,
∴∠DEC+∠OEC=∠DCE+∠OCE=∠ACB=90°,
∴∠OED=90°,即OE⊥DE,
∵E为⊙O上的点,
∴DE是⊙O的切线;
(2)解:①∵AC=3,
∴AD=DE=![]() AC=
AC=![]() ,
,
∵∠AEC=90°,
∴CE=![]() ,
,
∵∠BEC=90°,
∴∠CBE+∠OCE=90°,
∵∠ACB=90°,
∴∠CBE+∠DAE=90°,
∴∠OCE=∠DAE,
∵AD=DE,OC=OE,
∴∠OCE=∠OEC=∠DAE=∠DEA,
∴△OCE∽△DAE,
∴![]() ,
,
即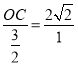 ,
,
解得:OC=![]() ,
,
故半径长为![]() ;
;
②当∠A=45°时,四边形OCDE是正方形;理由如下:
∵∠A=45°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵OB=OE,
∴∠OBE=∠OEB=45°,
∴∠COE=∠OBE+∠OEB=45°+45°=90°,
∵∠ACB=90°,∠OED=90°,
∴四边形OCDE是矩形,
∵OC=OE,
∴四边形OCDE是正方形;
故答案为:45°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax﹣3a(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=OC,直线y=﹣x与该抛物线交于E,F两点.
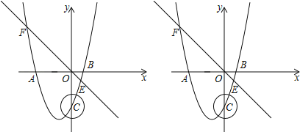
(1)求抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
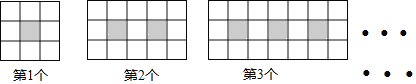
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
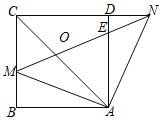
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE;
(3)MN和AC相交于O点,若BM=1,AB=3,试猜想线段OM,ON的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
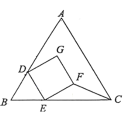
【题目】如图,等边三角形ABC和正方形DEFG按如图所示摆放,其中 D,E两点分别在AB,BC上,且BD=DE.若AB=12,DE=4,则△EFC的面积为( )
A.4B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
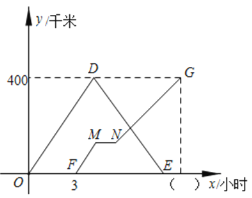
【题目】甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
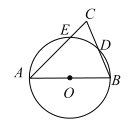
【题目】如图,AB为![]() 的直径,AC,BC分别交
的直径,AC,BC分别交![]() 于点E,D,
于点E,D,![]() ,
,![]() .现给出以下四个结论:①
.现给出以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的序号是________.(填写所有正确结论的序号)
.其中正确结论的序号是________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com