
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,MN与边AD交于点E.
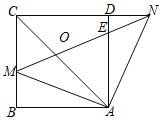
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE;
(3)MN和AC相交于O点,若BM=1,AB=3,试猜想线段OM,ON的数量关系并证明.
【答案】(1)见详解;(2)见详解;(3)ON=2OM,理由见详解
【解析】
(1)由正方形的性质可得AB=AD,由“ASA”可证△ABM≌△ADN,可得AM=AN;
(2)由题意可得∠CAM=∠NAD=22.5°,∠ACB=∠MNA=45°,即可证△AMC∽△AEN,即可证AM2=AEAC;
(3)先求出AM,进而求出MF=NF=BF=![]() ,再判断出△ABM∽△AFO,进而求出FO,即可得出结论.
,再判断出△ABM∽△AFO,进而求出FO,即可得出结论.
证明(1)∵四边形ABCD是正方形,
∴AB=AD,∠CAD=45°=∠ACB,∠BAD=90°=∠CDA=∠B,
∴∠BAM+∠MAD=90°,
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
∵AD=AB,∠ABC=∠ADN=90°,
∴△ABM≌△ADN(ASA)
∴AM=AN;
(2)∵AM=AN,∠MAN=90°
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN,
∴![]() ,
,
∴AMAN=ACAE,
∵AN=AM,
∴AM2=ACAE;
(3)ON=2OM,理由:如图,
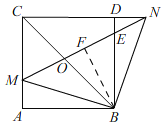
在Rt△ABM中,AM=1,AB=3,
根据勾股定理得,BM=![]() =
=![]() ,
,
过点B作BF⊥MN于F,
∴∠OFB=∠A=90°,
由(1)知,AM=AN,
∵∠MBN=90°,
∴FB=NF=MF=![]() =
=![]() ,∠MBF=45°,
,∠MBF=45°,
∵AC是正方形ABCD的对角线,
∴∠ABC=45°=∠MBF,
∴∠ABM=∠FBO,
∴△ABM∽△FBO,
∴![]() ,
,
∴![]() ,
,
∴FO=![]() ,
,
∴OM=MF﹣FO=![]() ,ON=NF+FO=
,ON=NF+FO=![]() ,
,
∴ON=2OM.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数学习中,我们经历了“确定函数表达式一利用函数图象研究其性质一运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象,同时我们也学习了绝对值的意义|a|![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b,当x=1时,y=﹣2;当x=0时,y=﹣1.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b,当x=1时,y=﹣2;当x=0时,y=﹣1.
(1)求这个函数的表达式;
(2)请你结合以下表格在坐标系中画出该函数的图象.

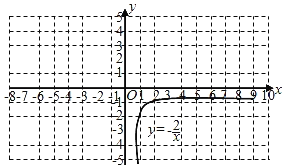
(3)观察这个函效图象,请写出该函数的两条性质;
(4)已知函数y=﹣![]() (x>0)的图象如图所示,请结合图象写出|kx﹣1|
(x>0)的图象如图所示,请结合图象写出|kx﹣1|![]() ﹣
﹣![]() ﹣b(x
﹣b(x![]() 0)的解集.
0)的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为进一步发展基础教育,自![]() 年以来加大了教育经费的投入,
年以来加大了教育经费的投入,![]() 年该地区投入教育经费
年该地区投入教育经费![]() 万元,
万元,![]() 年投入教育经费
年投入教育经费![]() 万元.
万元.
(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算![]() 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
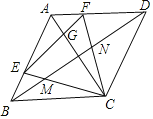
【题目】如图,已知边长为4的菱形ABCD中,AC=BC,E,F分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD与点M,N,给出下列结论:①∠AFC=∠AGE;②EF=BE+DF;③△ECF面积的最小值为3![]() ,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,以BC为直径作
,以BC为直径作![]() 交
交![]() 于点
于点![]() ,
,![]() 为AC边的中点,连接
为AC边的中点,连接![]() .
.
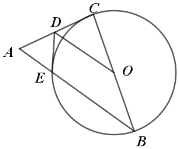
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)①若AC=3,AE=1,求![]() 的半径;
的半径;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 过
过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
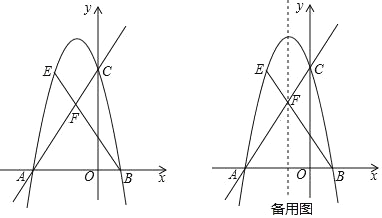
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在直线![]() 上方的抛物线上是否存在点
上方的抛物线上是否存在点![]() ,使
,使![]() 与
与![]() 的交点
的交点![]() 恰好为
恰好为![]() 的中点?如果存在,求出点
的中点?如果存在,求出点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
(3)若点![]() 在抛物线上且横坐标为
在抛物线上且横坐标为![]() ,点
,点![]() 是抛物线对称轴上一点,在抛物线上存在一点
是抛物线对称轴上一点,在抛物线上存在一点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?直接写出点
为顶点的四边形是平行四边形?直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com