
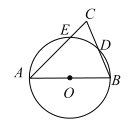
【题目】如图,AB为![]() 的直径,AC,BC分别交
的直径,AC,BC分别交![]() 于点E,D,
于点E,D,![]() ,
,![]() .现给出以下四个结论:①
.现给出以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的序号是________.(填写所有正确结论的序号)
.其中正确结论的序号是________.(填写所有正确结论的序号)
【答案】②④
【解析】
连结AD、BE,DE,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,加上CD=BD,根据等腰三角形的判定即可得到AB=AC;再根据等腰三角形的性质和三角形内角和定理可计算出∠BAC=40°;由AB为直径得到∠AEB=90°,则∠ABE=50°,根据圆周角定理可判断![]() ;接着证明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等线段代换即可得到CECA=2BD2.
;接着证明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等线段代换即可得到CECA=2BD2.
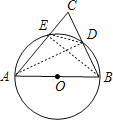
解:连结AD、BE,DE,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而CD=BD,
∴AB=AC,所以②正确;
∵∠C=70°,
∴∠ABC=∠C=70°,
∴∠BAC=40°,所以①错误;
∵AB为直径,
∴∠AEB=90°,
∴∠ABE=50°,
∴![]() ,所以③错误;
,所以③错误;
∵∠CED=∠CBA,
而∠C公共,
∴△CED∽△CBA,
∴![]() ,
,
∴CECA=CDCB,
∴CECA=BD2BD=2BD2,所以④正确.
故答案为②④.


科目:初中数学 来源: 题型:
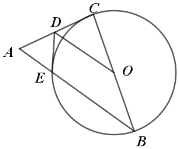
【题目】如图,已知在![]() 中,
中,![]() ,以BC为直径作
,以BC为直径作![]() 交
交![]() 于点
于点![]() ,
,![]() 为AC边的中点,连接
为AC边的中点,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)①若AC=3,AE=1,求![]() 的半径;
的半径;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.
(1)连接GD,求证![]() ;
;
(2)连接FC,求![]() 的值;
的值;
(3)如图2,将图1中正方形ABCD改为矩形ABCD,![]() ,
,![]() ,E是线段BC上一动点(不含端点B,C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.当点E由B向C运动时,判断
,E是线段BC上一动点(不含端点B,C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.当点E由B向C运动时,判断![]() 的值是否为定值?若是,求出该定值;若不是,请说明理由.
的值是否为定值?若是,求出该定值;若不是,请说明理由.
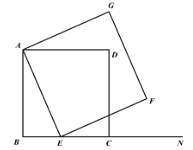
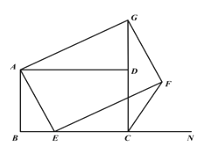
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB=26,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.
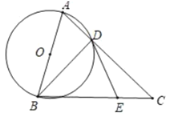
(1)证明:DE是⊙O的切线;
(2)若sin∠CDE=![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() 在
在![]() 轴正方向上取点
轴正方向上取点![]() ,使
,使![]() ;过点
;过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,在
,在![]() 轴正方向上取点
轴正方向上取点![]() ,使
,使![]() ;过点
;过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,在
,在![]() 轴正方向上取点
轴正方向上取点![]() ,使
,使![]() .记
.记![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() 面积为
面积为![]() ,则
,则![]() 等于( )
等于( )
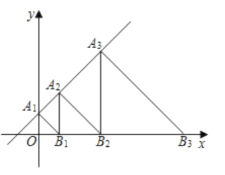
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com