
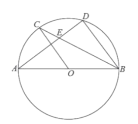
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】某校计划厂家购买A、B两种型号的电脑,已知每台A种型号电脑比每台B种型号电脑多01.万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同;
(1)求A、B两种型号电脑单价各为多少万元?
(2)学校预计用不多于9.2万元的资金购进20台电脑,其中A种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
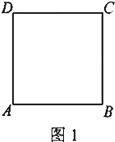
【题目】如图,正方形![]() 中,点
中,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,到达点
运动,到达点![]() 停止.作射线
停止.作射线![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转45°,与
逆时针旋转45°,与![]() 边交于点
边交于点![]() ,连接
,连接![]() .
.
(1)画图,完善图形.
(2)三条线段![]() ,
,![]() ,
,![]() 之间有无确定的数量关系?请说明理由.
之间有无确定的数量关系?请说明理由.
(3)过点![]() 作
作![]() 于
于![]() .若线段
.若线段![]() 的最大值为4,求点
的最大值为4,求点![]() 运动的路径长.
运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
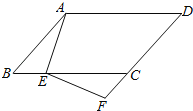
【题目】如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
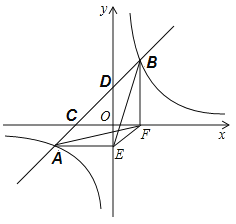
【题目】在一次数学课上,李老师出示一道开放题,让同学们依据已知条件写出正确结论,具体如下:如图,直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 和
和![]() 分别作
分别作![]() 轴和
轴和![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .若点
.若点![]() 坐标
坐标![]() ,请写出正确结论.聪明的强强很快写出了四个结论,其中不正确的结论是( )
,请写出正确结论.聪明的强强很快写出了四个结论,其中不正确的结论是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数学习中,我们经历了“确定函数表达式一利用函数图象研究其性质一运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象,同时我们也学习了绝对值的意义|a|![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b,当x=1时,y=﹣2;当x=0时,y=﹣1.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b,当x=1时,y=﹣2;当x=0时,y=﹣1.
(1)求这个函数的表达式;
(2)请你结合以下表格在坐标系中画出该函数的图象.

(3)观察这个函效图象,请写出该函数的两条性质;
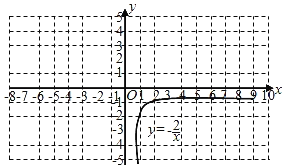
(4)已知函数y=﹣![]() (x>0)的图象如图所示,请结合图象写出|kx﹣1|
(x>0)的图象如图所示,请结合图象写出|kx﹣1|![]() ﹣
﹣![]() ﹣b(x
﹣b(x![]() 0)的解集.
0)的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com