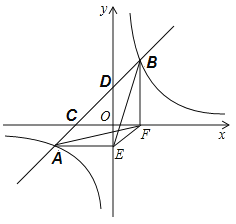
【题目】在一次数学课上，李老师出示一道开放题，让同学们依据已知条件写出正确结论，具体如下：如图，直线
与双曲线
相交于
，
两点，过点和分别作
轴和
轴的垂线，垂足分别为
，
，连接
，
，
，直线与轴和轴分别交于点
，
．若点坐标
，请写出正确结论．聪明的强强很快写出了四个结论，其中不正确的结论是（ ）
A.
B.
C.
D.
科目：初中数学 来源： 题型：
【题目】问题探究，
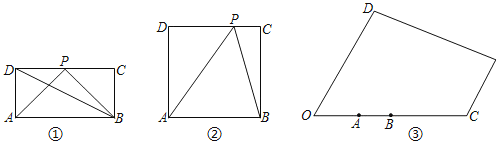
(1)如图①，在矩形ABCD中，AB＝2AD，P为CD边上的中点，试比较∠APB和∠ADB的大小关系，并说明理由；
(2)如图②，在正方形ABCD中，P为CD上任意一点，试问当P点位于何处时∠APB最大？并说明理由；
问题解决
(3)某儿童游乐场的平面图如图③所示，场所工作人员想在OD边上点P处安装监控装置，用来监控OC边上的AB段，为了让监控效果最佳，必须要求∠APB最大，已知：∠DOC＝60°，OA＝400米，AB＝200
米，问在OD边上是否存在一点P，使得∠APB最大，若存在，请求出此时OP的长和∠APB的度数；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】龙人文教用品商店欲购进
、
两种笔记本，用160元购进的种笔记本与用240元购进的种笔记本数量相同，每本种笔记本的进价比每本种笔记本的进价贵10元．
(1)求、两种笔记本每本的进价分别为多少元？
(2)若该商店准备购进、两种笔记本共100本，且购买这两种笔记本的总价不超过2650元，则至少购进种笔记本多少本?
查看答案和解析>>
科目：初中数学 来源： 题型：
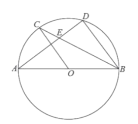
【题目】如图，
为⊙
的直径，
，
为圆上的两点，
，弦
，
相交于点
,
（1）求证：
（2）若
，
，求⊙的半径；
（3）在（2）的条件下，过点作⊙的切线，交
的延长线于点
，过点作
交⊙于
, 
两点（点在线段
上），求的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB、AC分别为⊙O的直径和弦，D为的中点，DE⊥AC于E，DE=6，AC=16．
（1）求证：DE是⊙O的切线．
（2）求直径AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读新知
一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个非零常数，这个数列就叫做等比数列．这个常数叫做等比数列的公比，公比通常用字母
表示（
）．
即：在数列
，
，
，…，
．（
为正整数）中，若
，
，…，则数列，，，…，．（为正整数）叫做等比数列．其中叫数列的首项，叫第二项，…，叫第项，叫做数列的公比．
例如：数列1，2，4，8，16，…是等比数列，公比
．
计算：求等比数列1，3，
，
，…，
的和．
解：令
，则
．
因此
．所以
．
即
．
学以致用
（1）选择题：下列数列属于等比数列的是（ ）
A．1，2，3，4，5 B．2，6，18，21，63
C．56，28，14，7，
D．－11，22，－33，44，－55
（2）填空题：已知数列，，，…，是公比为4的等比数列，若它的首项
，则它的第项等于_________．
（3）解答题：求等比数列1，5，
，
，…前2021项的和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知抛物线
与直线
都经过
，
两点，该抛物线的顶点为
．
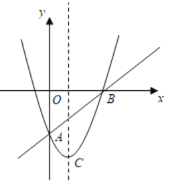
（1）求抛物线和直线
的解析式;
（2）设点
是直线下方抛物线上的一动点，求
面积的最大值，并求面积最大时，点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】按要求作图，不要求写作法，但要保留作图痕迹.
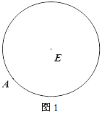
（1）如图1，A为圆E上一点，请用直尺（不带刻度）和圆规作出圆内接正方形；
（2）我们知道，三角形具有性质，三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高交于同一点，请运用上述性质，只用直尺（不带刻度）作图：
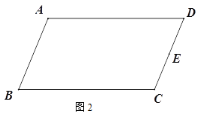
①如图2，在□ABCD中，E为CD的中点，作BC的中点F;
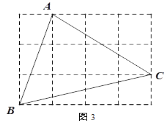
②图3，在由小正方形组成的网格中，的顶点都在小正方形的顶点上，作△ABC的高AH
查看答案和解析>>
科目：初中数学 来源： 题型：
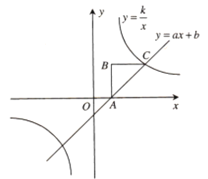
【题目】已知：如图，ABC是等腰直角三角形，∠B=90°，点B的坐标为(1,2)．反比例函数
的图象经过点C，一次函数y=ax+b的图象经A,C两点．
（1）求反比例函数和一次函数的关系式；
（2）直接写出不等式组0<ax+b≤
的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
