
【题目】问题探究,
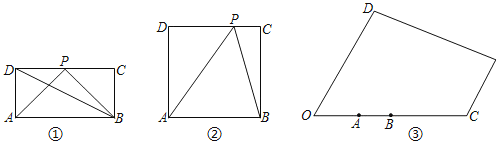
(1)如图①,在矩形ABCD中,AB=2AD,P为CD边上的中点,试比较∠APB和∠ADB的大小关系,并说明理由;
(2)如图②,在正方形ABCD中,P为CD上任意一点,试问当P点位于何处时∠APB最大?并说明理由;
问题解决
(3)某儿童游乐场的平面图如图③所示,场所工作人员想在OD边上点P处安装监控装置,用来监控OC边上的AB段,为了让监控效果最佳,必须要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
【答案】(1) 结论:∠APB>∠ADB ,理由见解析;(2) 当点P位于CD的中点时,∠APB最大,理由见解析;(3) 当经过A,B的⊙T与OD相切于P时,∠APB的值最大,理由见解析
【解析】
(1)作PH⊥AB于H,通过正方形和矩形的性质可得∠APB=90°,再根据∠ADB<90°,即可证明∠APB>∠ADB;
(2)假设P为CD的中点,如图②中,作△APB的外接圆⊙O,则此时CD切⊙O于点P,在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,根据∠AFB是△EFB的外角,可得∠AFB>∠AEB,再根据∠AFB=∠APB,从而可得∠APB>∠AEB,故点P位于CD的中点时,∠APB最大;
(3)作TH⊥OC于H,交OD于Q,连接TA,TB,OT.设TP=TA=TB=r,根据等边三角形的性质可得AH=HB=100![]() (m),再根据含30°角的直角三角形的性质可得AT=200
(m),再根据含30°角的直角三角形的性质可得AT=200![]() m,故AT=2AH,可得∠ATH=30°,即∠ATB=2∠ATH=60°,根据圆周角定理可得∠APB=
m,故AT=2AH,可得∠ATH=30°,即∠ATB=2∠ATH=60°,根据圆周角定理可得∠APB=![]() ∠ATB=30°,再根据含30°角的直角三角形的性质求出OQ和PQ的长度,再根据OP=OQ﹣PQ求解OP的长度即可.
∠ATB=30°,再根据含30°角的直角三角形的性质求出OQ和PQ的长度,再根据OP=OQ﹣PQ求解OP的长度即可.
解:(1)如图①中,结论:∠APB>∠ADB.
理由:作PH⊥AB于H.
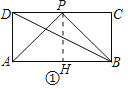
∵四边形ABCD是矩形,PH⊥AB,
∴∠ADP=∠DAH=∠AHP=90°,
∴四边形ADPH是矩形,
∵AB=CD=2AD,DP=PC,
∴DA=DP,
∴四边形ADPH是正方形,
∴∠APH=45°,同理可证∠BPH=45°,
∴∠APB=90°,
∵∠ADB<90°,
∴∠APB>∠ADB.
(2)当点P位于CD的中点时,∠APB最大,理由如下:
假设P为CD的中点,如图②中,作△APB的外接圆⊙O,则此时CD切⊙O于点P,
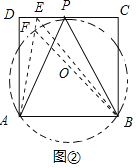
在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,
∵∠AFB是△EFB的外角,
∴∠AFB>∠AEB,
∵∠AFB=∠APB,
∴∠APB>∠AEB,
故点P位于CD的中点时,∠APB最大.
(3)如图③中,当经过A,B的⊙T与OD相切于P时,∠APB的值最大,
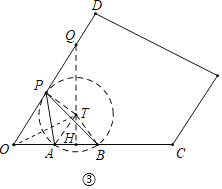
作TH⊥OC于H,交OD于Q,连接TA,TB,OT.设TP=TA=TB=r,
∵TA=TB,TH⊥AB,
∴AH=HB=100![]() (m),
(m),
∵∠OHQ=90°,∠O=60°,OH=OA+AH=(400+100![]() )(m),
)(m),
∴QH=![]() OH=(400
OH=(400![]() +300)(m),∠OQH=30°,
+300)(m),∠OQH=30°,
∴TQ=2PT=2r,
∵TH=![]() =
=![]() ,
,
∴2r+![]() =400
=400![]() +300,
+300,
整理得:3r2﹣(1600![]() +1200)r+60000+240000
+1200)r+60000+240000![]() =0,
=0,
∴(r﹣200![]() )(r﹣1000
)(r﹣1000![]() ﹣1200)=0,
﹣1200)=0,
∴r=200![]() 或1000
或1000![]() +1200(舍弃),
+1200(舍弃),
∴AT=200![]() m,
m,
∴AT=2AH,
∴∠ATH=30°,∠ATB=2∠ATH=60°,
∴∠APB=![]() ∠ATB=30°,
∠ATB=30°,
∴![]() ,
,![]()
∴OP=OQ﹣PQ=800+200![]() ﹣600=(200+200
﹣600=(200+200![]() )(m).
)(m).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
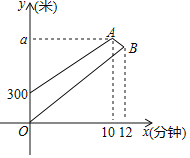
【题目】小明放学后从学校回家,出发![]() 分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发
分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发![]() 分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程
分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程![]() (米)与小强所用时间
(米)与小强所用时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求函数图象中![]() 的值;
的值;
(2)求小强的速度;
(3)求线段![]() 的函数解析式,并写出自变量的取值范围.
的函数解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
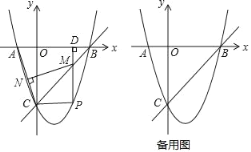
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=x﹣3经过B,C两点.
(1)求抛物线的解析式;
(2)点P是第四象限内抛物线上的动点,过点P作PD⊥x轴于点D,交直线BC于点M,连接AC,过点M作MN⊥AC于点N,设点P的横坐标为t.
①求线段MN的长d与t之间的函数关系式(不要求写出自变量t的取值范围);
②点Q是平面内一点,是否存在一点P,使以B,C,P,Q为顶点的四边形为矩形?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),则下列说法错误的是( )
A.a+c=0
B.无论a取何值,此二次函数图象与x轴必有两个交点,且函数图象截x轴所得的线段长度必大于2
C.当函数在x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D.当﹣1<m<n<0时,m+n<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
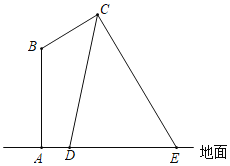
【题目】如图,某路灯在铅垂面内的示意图,灯柱AB的高为13米,灯杆BC与灯柱AB的夹角∠B=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为20米,已知tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,求灯杆BC的长度.
,求灯杆BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
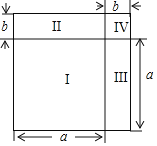
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为2,现将它沿AB方向平移1个单位,得到正六边形A′B′C′D′E′F′,则阴影部分A′BCDE′F′的面积是( )
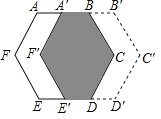
A.3![]() B.4
B.4![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
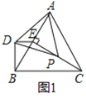
【题目】如图1,在等边![]() 和等边
和等边![]() 中,
中,![]() ,点P在
,点P在![]() 的高
的高![]() 上(点
上(点![]() 与点
与点![]() 不重合),点
不重合),点![]() 在点
在点![]() 的左侧,连接
的左侧,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
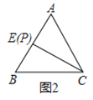
(2)当点![]() 与点
与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,请你在图2中作出图形,并求出
,请你在图2中作出图形,并求出![]() 的长;
的长;
(3)直接写出线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com