
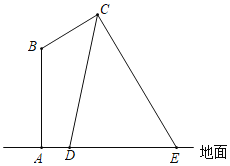
【题目】如图,某路灯在铅垂面内的示意图,灯柱AB的高为13米,灯杆BC与灯柱AB的夹角∠B=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为20米,已知tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,求灯杆BC的长度.
,求灯杆BC的长度.
【答案】灯杆CB的长度为2米
【解析】
过点C作CF⊥AE,交AE于点F,过点B作BG⊥CF,交CF于点G,设CF=7x,则EF=8x,根据锐角三角函数的性质求出x的值,即CG=1,再根据含30°角的直角三角形的性质求出BC的长度即可.
解:过点C作CF⊥AE,交AE于点F,过点B作BG⊥CF,交CF于点G,则FG=BA=13.
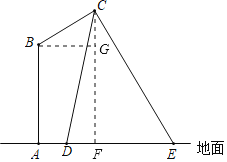
∵tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,
,
设CF=7x,则EF=8x.
在Rt△CDF中,
∵tan∠CDF=![]() ,
,
∴DF=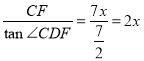 ,
,
∵DE=20,
∴2x+8x=20.
∴x=2.
∴CG=CF﹣GF=14﹣13=1.
∵∠ABC=120°,
∴∠CBG=∠ABC﹣∠ABG=120°﹣90°=30°.
∴CB=2CG=2,
答:灯杆CB的长度为2米.


科目:初中数学 来源: 题型:
【题目】如图,若点M是![]() 轴正半轴上任意一点,过点M作PQ∥
轴正半轴上任意一点,过点M作PQ∥![]() 轴,分别交函数
轴,分别交函数![]() 和
和![]() 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )

A.∠POQ不可能等于90°B.![]()
C.这两个函数的图象一定关于![]() 轴对称D.△POQ的面积是
轴对称D.△POQ的面积是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
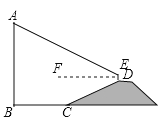
【题目】如图,![]() 是垂直于水平面的建筑物,为测量
是垂直于水平面的建筑物,为测量![]() 的高度,小红从建筑物底端
的高度,小红从建筑物底端![]() 出发,沿水平方向行走了52米到达点
出发,沿水平方向行走了52米到达点![]() ,然后沿斜坡
,然后沿斜坡![]() 前进,到达坡顶
前进,到达坡顶![]() 点处,
点处,![]() .在点
.在点![]() 处放置测角仪,测角仪支架
处放置测角仪,测角仪支架![]() 高度为0.8米,在
高度为0.8米,在![]() 点处测得建筑物顶端
点处测得建筑物顶端![]() 点的仰角
点的仰角![]() 为
为![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),斜坡
在同一平面内),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精确到个位)(参考数据:
的高度.(精确到个位)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
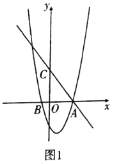
【题目】已知:如图1,抛物线![]() 是由抛物线
是由抛物线![]() 向右平移1个单位,再向下平移4个单位得到的,
向右平移1个单位,再向下平移4个单位得到的,![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),直线
的右侧),直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 点.
点.
(1)分别求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)如图2,已知![]() 点是线段
点是线段![]() 上任一点(不与
上任一点(不与![]() ,
,![]() 重合),过
重合),过![]() 点作
点作![]() 轴垂线,交抛物线
轴垂线,交抛物线![]() 于
于![]() 点.当
点.当![]() 在何处时,四边形
在何处时,四边形![]() 面积最大,求出此时
面积最大,求出此时![]() 点坐标及四边形
点坐标及四边形![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
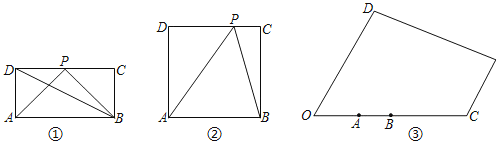
【题目】问题探究,
(1)如图①,在矩形ABCD中,AB=2AD,P为CD边上的中点,试比较∠APB和∠ADB的大小关系,并说明理由;
(2)如图②,在正方形ABCD中,P为CD上任意一点,试问当P点位于何处时∠APB最大?并说明理由;
问题解决
(3)某儿童游乐场的平面图如图③所示,场所工作人员想在OD边上点P处安装监控装置,用来监控OC边上的AB段,为了让监控效果最佳,必须要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
米,问在OD边上是否存在一点P,使得∠APB最大,若存在,请求出此时OP的长和∠APB的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
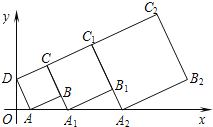
【题目】在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(3,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C,延长C1B1交x轴于点A2;作第3个正方形A2B2C2C1,…按这样的规律进行下去,第5个正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
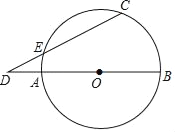
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则弧BC的长度为( )
A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们的生活水平的提高,家用轿车越来越多地进入家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣9 | ﹣13 | 0 | ﹣14 | ﹣16 | +33 | +19 |
(1)求出这7天的行驶路程中最多的一天比最少的一天多行驶多少千米?
(2)若每行驶100km需用汽油8升,每升汽油6.5元,计算小明家这7天的汽油费用共是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com