
【题目】如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE⊥AC于E,DE=6,AC=16.
(1)求证:DE是⊙O的切线.
(2)求直径AB的长.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
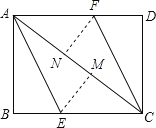
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足怎样数量关系时,四边形AECF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
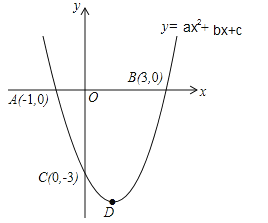
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)直线![]() 平行于
平行于![]() 轴,与抛物线交于
轴,与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,求线段
,求线段![]() 的长;
的长;
(3)点![]() 是该抛物线上一点,且在第一象限内,联结
是该抛物线上一点,且在第一象限内,联结![]() 、
、![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
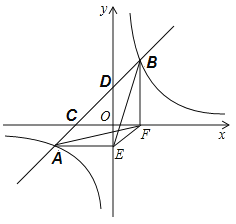
【题目】在一次数学课上,李老师出示一道开放题,让同学们依据已知条件写出正确结论,具体如下:如图,直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 和
和![]() 分别作
分别作![]() 轴和
轴和![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .若点
.若点![]() 坐标
坐标![]() ,请写出正确结论.聪明的强强很快写出了四个结论,其中不正确的结论是( )
,请写出正确结论.聪明的强强很快写出了四个结论,其中不正确的结论是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,![]() 点朝上是必然事件
点朝上是必然事件
B.了解一批灯泡的使用寿命,适合用普查的方式.
C.从五张分别写着![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的卡片中随机抽取
的卡片中随机抽取![]() 张,是无理数的概率是
张,是无理数的概率是![]() .
.
D.甲乙两人在相同条件下各射击![]() 次,他们的成绩平均数相同,方差分别是
次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定.
,则甲的射击成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
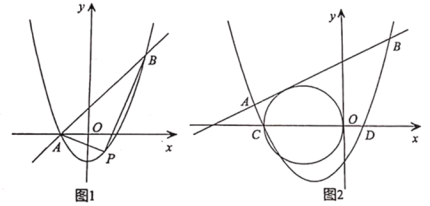
【题目】在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A、B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com