
【题目】在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A、B两点,点A在点B的左侧.
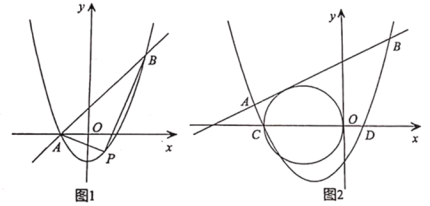
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,说明理由.
【答案】(1)A(-1,0),B(2,3);(2)△ABP面积最大值为![]() ,此时点P坐标为(
,此时点P坐标为(![]() ,﹣
,﹣![]() );(3)存在,k=
);(3)存在,k=![]() 时,使得直线y=kx+1与以OC为直径的圆相切.
时,使得直线y=kx+1与以OC为直径的圆相切.
【解析】
(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;
(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)设直线y=kx+1与以O、C为直径的圆相切的切点为Q,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与抛物线交于C点,此时不存在.
解:(1)当k=1时,抛物线解析式为y=x2-1,直线解析式为y=x+1.
联立两个解析式,得:x2-1=x+1,
解得:x=-1或x=2,
当x=-1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(-1,0),B(2,3).
(2)设P(x,x2-1),
如答图1所示,过点P作PF//y轴,交直线AB于点F,则F(x,x+1).
∴PF=yF﹣yP=(x+1)﹣(x2﹣1)=﹣x2+x+2.
S△ABP=S△PFA+S△PFB=![]() PF(xF﹣xA)+
PF(xF﹣xA)+![]() PF(xB﹣xF)=
PF(xB﹣xF)=![]() PF(xB﹣xA)=
PF(xB﹣xA)=![]() PF
PF
∴S△ABP=![]() (﹣x2+x+2)=﹣
(﹣x2+x+2)=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .当x=
.当x=![]() 时,yP=x2﹣1=﹣
时,yP=x2﹣1=﹣![]() .
.
∴△ABP面积最大值为![]() ,此时点P坐标为(
,此时点P坐标为(![]() ,﹣
,﹣![]() ).
).
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(﹣![]() ,0),F(0,1),OE=
,0),F(0,1),OE=![]() ,OF=1.
,OF=1.
在Rt△EOF中,由勾股定理得:EF=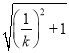 =
=![]() . 令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1. ∴C(﹣k,0),OC=k.
. 令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1. ∴C(﹣k,0),OC=k.
(Ⅰ)设直线y=kx+1与以O、C为直径的圆相切的切点为Q,如答图2所示,

则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.
设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=![]() .∴EN=OE﹣ON=
.∴EN=OE﹣ON=![]() ﹣
﹣![]() .
.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,∴△EQN∽△EOF,
∴![]() =
=![]() ,即
,即![]() =
=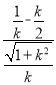 解得:k=±
解得:k=±![]() ,∵k>0,∴k=
,∵k>0,∴k=![]() .
.
∴存在实数k使得直线y=kx+1与以OC为直径的圆相切,
此时k=![]() .
.
(Ⅱ)若直线AB过点C时,此时直线与以OC为直径的圆要相切,必有AB⊥x轴,
而直线AB的解析式为y=kx+1,∴不可能相切.
综上所述,k=![]() 时,使得直线y=kx+1与以OC为直径的圆相切.
时,使得直线y=kx+1与以OC为直径的圆相切.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE⊥AC于E,DE=6,AC=16.
(1)求证:DE是⊙O的切线.
(2)求直径AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
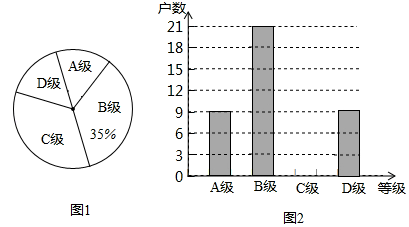
(1)本次抽样调查的养殖户的总户数是 ;把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?
(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
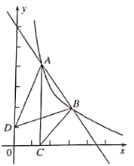
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
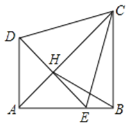
【题目】将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ,其中正确的结论是____________ (填写所有正确结论的序号)
,其中正确的结论是____________ (填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC是等腰直角三角形,∠B=90°,点B的坐标为(1,2).反比例函数![]() 的图象经过点C,一次函数y=ax+b的图象经A,C两点.
的图象经过点C,一次函数y=ax+b的图象经A,C两点.
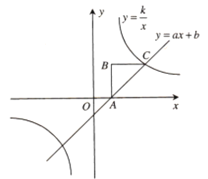
(1)求反比例函数和一次函数的关系式;
(2)直接写出不等式组0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
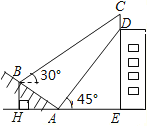
【题目】如图,某大楼的顶部有一块广告牌![]() ,小背在山坡的坡脚
,小背在山坡的坡脚![]() 处测得广告牌底部的仰角为45°,沿坡面
处测得广告牌底部的仰角为45°,沿坡面![]() 向上走到
向上走到![]() 处测得广告牌顶部
处测得广告牌顶部![]() 的仰角为30°.已知山坡
的仰角为30°.已知山坡![]() 的坡度为
的坡度为![]() ,
,![]() 米,
米,![]() 米.
米.
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)求广告牌![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF,连接CF交线段AB于点G,交AD于点H、连接EG.
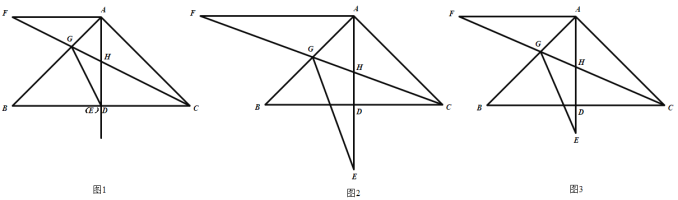
特例分析:
(1)如图1,当点E与点D重合时,“智敏”小组提出如下问题,请你解答:
①求证:AF=CD;
②用等式表示线段CG与EG之间的数量关系为:_______;
拓展探究:
(2)如图2,当点E在线段AD的延长线上,且DE=AD时,“博睿”小组发现CF=2EG.请你证明;
(3)如图3,当点E在线段AD的延长线上,且AE=AB时,![]() 的值为_______;
的值为_______;
推广应用:
(4)当点E在射线AD上运动时,![]() ,则
,则![]() 的值为______用含m.n的式子表示).
的值为______用含m.n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大建设资金的投入.
(1)机场建设项目中所有6个机场投入的建设资金金额统计如下图,已知机场![]() 投入的建设资金金额是机场
投入的建设资金金额是机场![]() 、
、![]() 所投入建设资金金额之和的三分之二,求机场
所投入建设资金金额之和的三分之二,求机场![]() 投入的建设资金金额是多少亿元?并补全条形统计图.
投入的建设资金金额是多少亿元?并补全条形统计图.
(2)将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表,根据扇形统计图及统计表中的信息,求得![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .(请直接填写计算结果)
.(请直接填写计算结果)

铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
投入资金(亿元) | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com