
【题目】将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ,其中正确的结论是____________ (填写所有正确结论的序号)
,其中正确的结论是____________ (填写所有正确结论的序号)
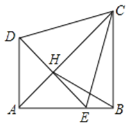
【答案】①②③④
【解析】
利用等腰直角三角形的性质得出∠DAC=∠BAC即可判断出①正确;再用等腰直角三角形的内角的关系即可得出∠DCE=60°,即可得出②正确,判断出∠BCD=75°=∠BEC即可判断出③正确,设出AH=x,利用等腰直角三角形和等边三角形的性质即可得出CH,EH,AB,BE最后用三角形的面积公式即可得出④正确.
∵△ABC和△ADE是等腰直角三角形,
∴∠BAC=∠ACB=45°,∠DAE=90°,
∴∠DAC=∠BAC=45°,
∵AD=AE,
∴AC垂直平分DE,∴①正确,
∵AC垂直平分DE,
∴DC=EC,∠DAC=∠EAC,
∵∠BCE=15°,
∴∠ACE=30°,
∴∠DCE=2∠ACE=60°,
∴△CDE是等边三角形,∴②正确;
∵∠DCE=60°,∠BCE=15°,
∴∠BCD=75°,
∵∠BEC=90°15°=75°,
∴∠BCD=∠BEC,
在Rt△BCE中,tan∠BEC=![]() ,
,
∴tan∠BCD=![]() ,∴③正确;
,∴③正确;
设AH=x,
在Rt△AEH中,HE=AH=x,AE=![]() x,
x,
在Rt△CEH中,∠ECH=30°,
∴CH=EH÷tan30°=![]() EH=
EH=![]() x,CE=2HE=2x,
x,CE=2HE=2x,
∴AC=AH+CH=(![]() +1)x,
+1)x,
在Rt△ABC中,BC=AB=AC×sin45°=![]() AC=
AC=![]() (
(![]() +1)x=
+1)x=![]() x,
x,
∴BE=ABAE=![]() x,
x,
∴S△BCE=![]() BEBC=
BEBC=![]() ×
×![]() x
x![]() x
x![]() x2
x2
S△EHC=![]() EHCH=
EHCH=![]() x
x![]() x=
x=![]() x2,
x2,
∴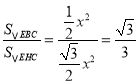 ,∴④正确,
,∴④正确,
即:正确的有①②③④,
故答案为:①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)直线![]() 平行于
平行于![]() 轴,与抛物线交于
轴,与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,求线段
,求线段![]() 的长;
的长;
(3)点![]() 是该抛物线上一点,且在第一象限内,联结
是该抛物线上一点,且在第一象限内,联结![]() 、
、![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
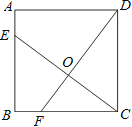
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
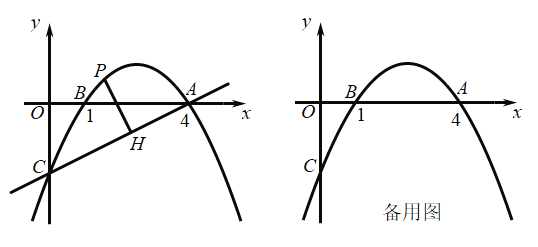
查看答案和解析>>
科目:初中数学 来源: 题型:
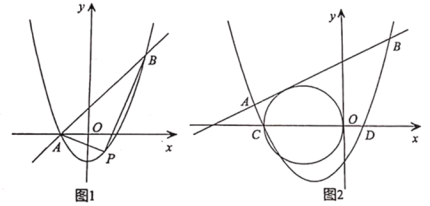
【题目】在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A、B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润![]() (元)与批发单价
(元)与批发单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元;
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围.(每天的总成本![]() 每瓶的成本
每瓶的成本![]() 每天的经销量)
每天的经销量)
查看答案和解析>>
科目:初中数学 来源: 题型:
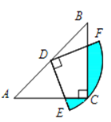
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
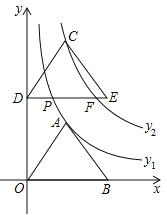
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .把
.把![]() 向上平移
向上平移![]() 个单位长度得到
个单位长度得到![]() .反比例函数
.反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设反比例函数![]() 的图象交线段
的图象交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合) .当
重合) .当![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com