
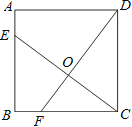
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.
∵AE=BF=1,∴BE=CF=4-1=3.
在△EBC和△FCD中,∵BC=CD,∠B=∠DCF,BE=CF,∴△EBC≌△FCD(SAS).
∴∠CFD=∠BEC.∴∠BCE+∠BEC=∠BCE+∠CFD=90°.
∴∠DOC=90°.故①正确.
如图,连接DE
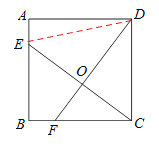
若OC=OE,∵DF⊥EC,∴CD=DE.
∵CD=AD<DE(矛盾),故②错误.
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC.
∴tan∠OCD=tan∠DFC=![]() .故③正确.
.故③正确.
∵△EBC≌△FCD,∴S△EBC=S△FCD.
∴S△EBC-S△FOC=S△FCD-S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
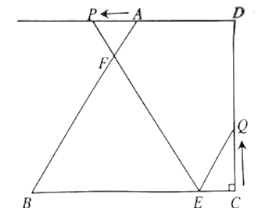
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
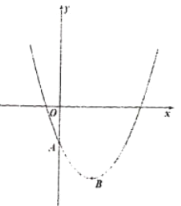
【题目】在平面直角坐标系中,已知如图所示的抛物线顶点![]() 的坐标为
的坐标为![]() ,且过点
,且过点![]() .
.
(1)求该抛物线的解析式;
(2)若点![]() 为抛物线对称轴右侧、
为抛物线对称轴右侧、![]() 轴下方一点,当
轴下方一点,当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)平移(1)中的抛物线,记平移后抛物线的顶点为![]() ,顶点
,顶点![]() 在直线
在直线![]() 上滑动,且平移后的抛物线与直线
上滑动,且平移后的抛物线与直线![]() 交于另一点
交于另一点![]() ,若点
,若点![]() 为平移前(1)中抛物线上的点,则当以
为平移前(1)中抛物线上的点,则当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
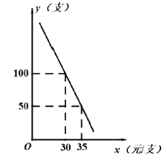
【题目】某网店专售一款电动牙刷,其成本为 20 元/支,销售中发现该商品每天的销售量 ![]() (支)与销售单价
(支)与销售单价 ![]() (元/支)之间存在如图所示的关系.
(元/支)之间存在如图所示的关系.
(1)求出 ![]() 与
与 ![]() 的函数关系式(不需要写出自变量取值范围);
的函数关系式(不需要写出自变量取值范围);
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出 200元捐赠给武汉,为了保证捐款后每天剩余利润不低于 550 元,试确定该款电动牙刷销售单价![]() 的取值范围?
的取值范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销-种进价为每千克50元的水产品,据市场分析,每千克售价为60元时,月销售量为![]() ,销售单价每涨1元时,月销售量就减少
,销售单价每涨1元时,月销售量就减少![]() ,针对这种情况,请解答以下问题:
,针对这种情况,请解答以下问题:
(1)当销售单价定为65元时,计算销售量和月销售利润;
(2)若想在月销售成本不超过12000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com