【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克） | … | 34.8 | 32 | 29.6 | 28 | … |
售价x（元/千克） | … | 22.6 | 24 | 25.2 | 26 | … |
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？
【答案】（1）当天该水果的销售量为33千克；（2）如果某天销售这种水果获利150元，该天水果的售价为25元．
【解析】
（1）根据表格内的数据，利用待定系数法可求出y与x之间的函数关系式，再代入x=23.5即可求出结论；
（2）根据总利润
每千克利润
销售数量，即可得出关于x的一元二次方程，解之取其较小值即可得出结论．
（1）设y与x之间的函数关系式为y=kx+b，
将（22.6，34.8）、（24，32）代入y=kx+b，
，解得：
，
∴y与x之间的函数关系式为y=﹣2x+80．
当x=23.5时，y=﹣2x+80=33．
答：当天该水果的销售量为33千克．
（2）根据题意得：（x﹣20）（﹣2x+80）=150，
解得：x1=35，x2=25．
∵20≤x≤32，
∴x=25．
答：如果某天销售这种水果获利150元，那么该天水果的售价为25元．
科目：初中数学 来源： 题型：
【题目】2019年2月14日，备受关注的《成都市中小学课后服务实施意见》正式出台.某区为了解“家长更希望如何安排孩子放学后的时间”，对该区七年级部分家长进行了一次问卷调查（每位同学只选择一位家长参与调查），将调查结果（
.回家，家人陪伴；
.学校课后延时服务；
.校外培训机构；
.社会托管班）绘制成以下两幅不完整的统计图.请根据图中提供的信息，解答下列问题：
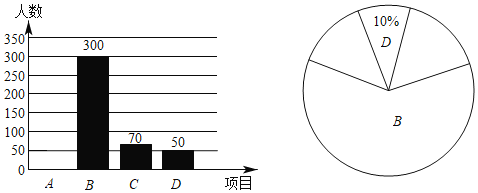
（1）本次调查的家长总人数为 ；
（2）补全条形统计图：扇形统计图中，类所对应的圆心角为 度；
（3）若该区共有七年级学生
人，则愿意参加“学生课后延时服务”的人数大概是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
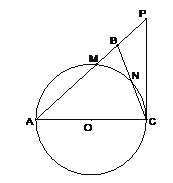
【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP.
（1）求证：直线CP是⊙O的切线；
（2）若BC=2
，sin∠BCP=
，求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在 ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF,其中正确结论的个数共有（ ）.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
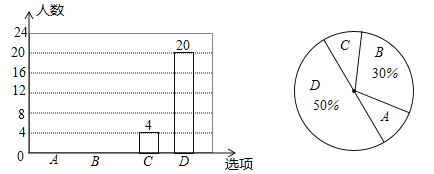
【题目】全面二孩政策于2016年1月1日正式实施，黔南州某中学对八年级部分学生进行了随机问卷调查，其中一个问题“你爸妈如果给你添一个弟弟（或妹妹），你的态度是什么？”共有如下四个选项（要求仅选择一个选项）：
A．非常愿意 B．愿意 C．不愿意 D．无所谓
如图是根据调查结果绘制的两幅不完整的统计图，请结合图中信息解答以下问题：
（1）试问本次问卷调查一共调查了多少名学生？并补全条形统计图；
（2）若该年级共有450名学生，请你估计全年级可能有多少名学生支持（即态度为“非常愿意”和“愿意”）爸妈给自己添一个弟弟（或妹妹）？
（3）在年级活动课上，老师决定从本次调查回答“不愿意”的同学中随机选取2名同学来谈谈他们的想法，而本次调查回答“不愿意”的这些同学中只有一名男同学，请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的一元二次方程
（1）求证：方程总有两个不相等的实数根。
（2）m为何整数时，此方程的两个根都是正整数？
（3）若△ABC的两边AB,AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求m的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
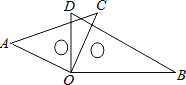
【题目】如图,将一副三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=()度。
A. 小于180 B. 大于180 C. 等于180 D. 无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，DE⊥AC，垂足为点E，∠AGF＝∠ABC，∠BFG+∠BDE＝180°，
求证：BF⊥AC．
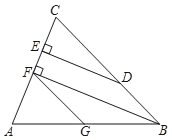
请完成下面的证明的过程，并在括号内注明理由．
证明：∵∠AGF＝∠ABC（已知）
∴FG∥ （ ）
∴∠BFG＝∠FBC（ ）
∵∠BFG+∠BDE＝180°（已知）
∴∠FBC+∠BDE＝180°（ ）
∴BF∥DE（ ）
∴∠BFA＝ （两直线平行，同位角相等）
∵DE⊥AC（已知）
∴∠DEA＝90°（ ）
∴∠BFA＝90°（等量代换）
∴BF⊥AC（垂直的定义）
查看答案和解析>>
科目：初中数学 来源： 题型：
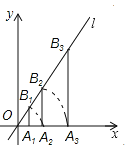
【题目】如图，点A1的坐标为（2，0），过点A1作x轴的垂线交直线l：y=
x于点B1，以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，以OB2的长为半径画弧交x轴正半轴于点A3；…．按此作法进行下去，则
的长是_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com