
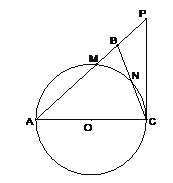
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
【答案】详见解析.
【解析】试题分析: (1)欲证明直线CP是![]() 的切线,只需证得CP⊥AC;
的切线,只需证得CP⊥AC;
(2)利用正弦三角函数的定义求得 ![]() 的直径
的直径![]() 则
则 ![]() 的半径为
的半径为![]()
如图,过点B作BD⊥AC于点D,构建相似三角形:△CAN∽△CBD,所以根据相似三角形的对应边成比例求得线段![]() ;然后在Rt△BCD中,,利用勾股定理可以求得
;然后在Rt△BCD中,,利用勾股定理可以求得![]() 所以利用平行线分线段成比例分别求得线段
所以利用平行线分线段成比例分别求得线段![]() 的长度.即可求出
的长度.即可求出![]() 的周长.
的周长.
试题解析:(1)证明:连接AN,
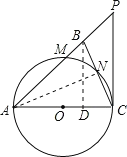
∵∠ABC=∠ACB,∴AB=AC,
∵AC是![]() 的直径,∴AN⊥BC,
的直径,∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=![]() ,
,
∴∠BCP+∠ACN=![]() ,
,
∴CP⊥AC,
∵OC是![]() 的半径
的半径
∴CP是![]() 的切线;
的切线;
(2)![]()
![]() ∴AC=5,
∴AC=5,
∴![]() 的半径为
的半径为![]()
如图,过点B作BD⊥AC于点D.
由(1)得![]()
在Rt△CAN中,![]()
在△CAN和△CBD中,
![]()
∴△CAN∽△CBD,
![]()
∴BD=4.
在Rt△BCD中,![]()
∴AD=ACCD=52=3,
∵BD∥CP,
![]()
![]()
∴△APC的周长是AC+PC+AP=20.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
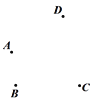
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有两个不相等的实数根?
(3)若x1,x2是方程的两个实数根,且xx2+x1x=-![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(﹣1,﹣4),C(2,﹣3).
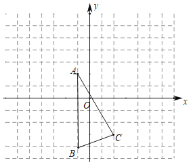
(1)将△ABC先向右平移4个单位,再向上平移6个单位,得到△A1B1C1,作出△A1B1C1,线段AC在平移过程中扫的面积为 ;
(2)作出△A1B1C1关于y轴对称的图形△A2B2C2,则坐标C2为 ;
(3)若△ABD与△ABC全等,则点D的坐标为 (点C与点D不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
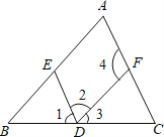
【题目】请结合图形完成下列推理过程:
(1)∵∠2+∠4=180°,
∴DE∥AC (______).
(2)∵∠1=∠C,
∴DE∥______(______).
(3)∵AB∥DF,
∴∠2=∠______(______).
(4)∵______∥______,
∴∠B=∠3 (______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
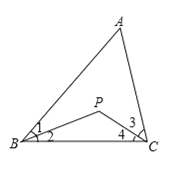
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
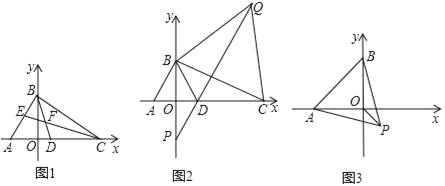
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com