
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
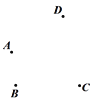
科目:初中数学 来源: 题型:
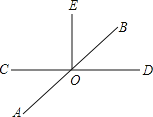
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面材料:如果![]() (
(![]() )的b次幂等于N,即有指数式
)的b次幂等于N,即有指数式![]() ,那么数b叫做以
,那么数b叫做以![]() 为底N的对数,
为底N的对数,
记作:对数式: ![]()
例如:
(1)因为指数式![]() ,所以以2为底,4的对数是2,对数式记作:
,所以以2为底,4的对数是2,对数式记作:![]()
(2)因为指数式![]() ,所以以4为底,16的对数是2,对数式记作:
,所以以4为底,16的对数是2,对数式记作:![]()
1. 请根据上面阅读材料将下列指数式改为对数试:(1)![]() ;(2)
;(2)![]()
2. 将下列对数式改为指数式:(1)![]() ;(2)
;(2)![]()
3.计算 :![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
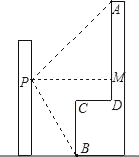
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
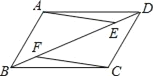
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课上老师提出一个问题:“如图,已知![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.”
的度数.”
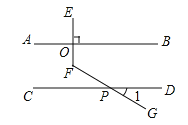
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
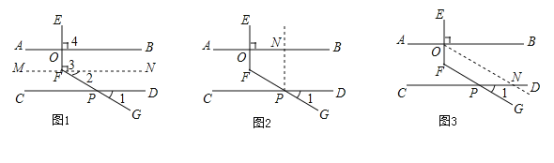
(1)补全甲同学的分析思路.
辅助线:过点![]() 作
作![]() .
.
分析思路:
①欲求∠EFG的度数,由图可知只需转化为求________和___________的度数之和;
②由辅助线作图可知![]() ;
;
③由![]() ,
,![]() 推出_________________,由此可推出
推出_________________,由此可推出![]() ;
;
④由已知![]() ,可得
,可得![]() ,所以可得
,所以可得![]() 的度数,从而可求
的度数,从而可求![]() 的度数.
的度数.
(2)请你根据乙同学所画的辅助线,补全求解过程.
解:过![]() 作___________________,交
作___________________,交![]() 于点
于点![]() .
.
![]() ___________________________
___________________________![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (_______________________).
(_______________________).
![]() .
.
![]() (____________________________),
(____________________________),
![]() ,
,
![]() _______________________.
_______________________.
(3)请你根据丙同学所画的辅助线,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月14日,备受关注的《成都市中小学课后服务实施意见》正式出台.某区为了解“家长更希望如何安排孩子放学后的时间”,对该区七年级部分家长进行了一次问卷调查(每位同学只选择一位家长参与调查),将调查结果(![]() .回家,家人陪伴;
.回家,家人陪伴;![]() .学校课后延时服务;
.学校课后延时服务;![]() .校外培训机构;
.校外培训机构;![]() .社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
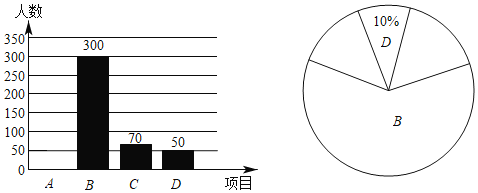
(1)本次调查的家长总人数为 ;
(2)补全条形统计图:扇形统计图中,![]() 类所对应的圆心角为 度;
类所对应的圆心角为 度;
(3)若该区共有七年级学生![]() 人,则愿意参加“学生课后延时服务”的人数大概是多少?
人,则愿意参加“学生课后延时服务”的人数大概是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
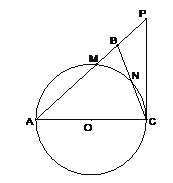
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com