【题目】观察下列等式：
(x-1)(x+1)=x2-1；
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1；
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______．
运用上述规律，试求：
(2)219+218+217+…+23+22+2+1．
(3)52018+52017+52016+…+53+52+5+1．
【答案】(1)xn+1-1；(2)220-1；(3)
(52019-1)．
【解析】
(1)根据已知算式得出的规律求出即可；
(2)先变形，再根据已知算式得出的规律求出即可；
(3)先变形，再根据已知算式得出的规律求出即可．
解：(1)(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1，
故答案为：xn+1-1；
(2)219+218+217+…+23+22+2+1
=(2-1)×(219+218+217+…+23+22+2+1)
=220-1；
(3)52018+52017+52016+…+53+52+5+1
=(5-1)×(52018+52017+52016+…+53+52+5+1)×
=(52019-1)．
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案科目：初中数学 来源： 题型：
【题目】如图AB是半圆O的直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下5个结论：①OD∥AC；②AC＝2CD；③2CD2＝CEAB；④S△AEC＝2S△DEO；⑤线段OD是DE与DA的比例中项．其中正确结论的序号( )
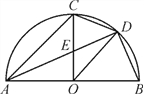
A. ①②③ B. ①④⑤ C. ①③④ D. ①③④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．
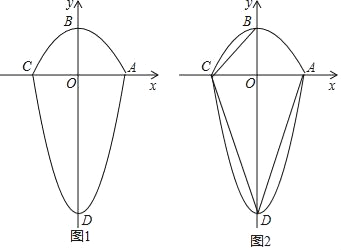
（1）直接写出这两个二次函数的表达式；
（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；
（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线L：y=3x+2，现有下列命题：
①过点P（-1，1）与直线L平行的直线是y=3x+4；②若直线L与x轴、y轴分别交于A、B两点，则AB=
；③若点M（-
，1），N（a，b）都在直线L上，且a>-，则b>1； ④若点Q到两坐标轴的距离相等，且Q在L上，则点Q在第一或第二象限。其中正确的命题是_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)平面上有四个点A，B，C，D，按照以下要求作图：
①作直线AD；
②作射线CB交直线AD于点E；
③连接AC，BD交于点F；
(2)图中共有 条线段；
(3)若图中F是AC的一个三等分点，AF＜FC，已知线段AC上所有线段之和为18，求AF长.
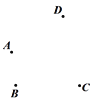
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】推理探索：（1）数轴上点
、
、
、
、
分别表示数0、 2 、3、5、 4 ，解答下列问题．
①画出数轴表示出点、、、、；
②、两点之间的距离是 ；
③、 两点之间的距离是 ；
④、 两点之间的距离是 ；
（2）请思考，若点表示数
且
，点 表示数
，且 
，则用含 ， 的代数式表示 
、两点 间的距离是 ；
（3）请归纳，若点 表示数
，点 表示数
，则 、 两点间的距离用含、的代数式表示是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在正方形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E.若AD＝8cm，则OE的长为（ ）
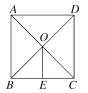
A. 3cm B. 4cm C. 6cm D. 8cm
查看答案和解析>>
科目：初中数学 来源： 题型：
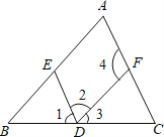
【题目】请结合图形完成下列推理过程：
（1）∵∠2+∠4=180°，
∴DE∥AC （______）．
（2）∵∠1=∠C，
∴DE∥______（______）．
（3）∵AB∥DF，
∴∠2=∠______（______）．
（4）∵______∥______，
∴∠B=∠3 （______）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
