
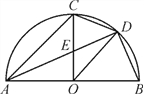
【题目】如图AB是半圆O的直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:①OD∥AC;②AC=2CD;③2CD2=CEAB;④S△AEC=2S△DEO;⑤线段OD是DE与DA的比例中项.其中正确结论的序号( )
A. ①②③ B. ①④⑤ C. ①③④ D. ①③④⑤
【答案】C
【解析】
根据“圆的相关性质和相似三角形的判定与性质”结合已知条件进行分析判断即可.
(1)∵AD平均∠CAB,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴OD∥AC,即结论①成立;
(2)连接BC,∵OC⊥AB,
∴AC=BC,
∵AD平均∠BAC,
∴点D是![]() 的中点,
的中点,
∴CD=BD,
∵在△BCD中,CD+BD>BC,
∴2CD>BC,
∴2CD>AC,即结论②不成立;
(3)∵OC⊥AB,
∴∠AOC=∠BOC=90°,
∴∠CDE=![]() ∠AOC=45°,
∠AOC=45°,
∵点D是![]() 的中点,
的中点,
∴∠COD=![]() ∠BOC=45°,
∠BOC=45°,
∴∠CDE=∠COD,
又∵∠DCE=∠OCD,
∴△CDE∽△COD,
∴CD:CO=CE:CD,
∴CD2=CE·CO,
∵CO=AO=![]() AB,
AB,
∴CD2=CE·![]() AB,
AB,
∴2CD2=CE·AB,即结论③成立;
(4)∵AC∥OD,
∴△ACE∽△DOE,
∴S△ACE:S△DOE=![]() ,
,
∵△AOC中,∠AOC=90°,OA=OC,
∴AC:OC=![]() ,
,
∴S△ACE:S△DOE=2:1,
∴S△ACE=2S△DOE,即结论④成立;
(5)∵在△AOD中,AO=DO,∠AOD=∠AOC+∠COD=135°,
∴∠OAD=∠ODA=22.5°,
∵在△DOE中,∠DOE=45°,∠ODE=22.5°,
∴∠DEO=180°-45°-22.5°=112.5°,
由此可知△AOD是等腰三角形,而△DOE不是等腰三角形,
∴△AOD和△OED不可能相似,
∴无法证明OD是AD和DE的比例中项,即结论⑤不成立.
综上所述,上述5个结论中,成立的是①③④.
故选C.



科目:初中数学 来源: 题型:
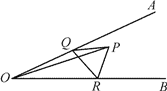
【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
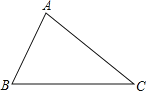
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
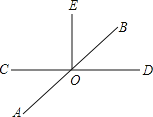
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c>0;②a-b+c>1;③abc>0;④4a-2b+c<1;⑤b+2a=0. 其中所有正确的结论是______.(填序号)
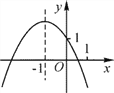
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com