
【题目】如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).
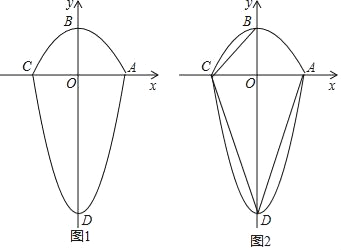
(1)直接写出这两个二次函数的表达式;
(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;
(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标
【答案】(1)y1=﹣x2+1,y2=3x2﹣3;(2)存在,理由见解析;(3)(0,﹣![]() )或(
)或(![]() ,﹣1)或(1,﹣
,﹣1)或(1,﹣![]() )或(﹣
)或(﹣![]() ,﹣2).
,﹣2).
【解析】(1)利用待定系数法即可得出结论;
(2)先确定出MM'=(1-m2)-(3m2-3)=4-4m2,进而建立方程2m=4-4m2,即可得出结论;
(3)先利用勾股定理求出AD=![]() ,同理:CD=
,同理:CD=![]() ,BC=
,BC=![]() ,再分两种情况:
,再分两种情况:
①如图1,当△DBC∽△DAE时,得出![]() ,进而求出DE=
,进而求出DE=![]() ,即可得出E(0,-
,即可得出E(0,-![]() ),
),
再判断出△DEF∽△DAO,得出![]() ,求出DF=
,求出DF=![]() ,EF=
,EF=![]() ,再用面积法求出E'M=
,再用面积法求出E'M=![]() ,即可得出结论;
,即可得出结论;
②如图2,当△DBC∽△ADE时,得出![]() ,求出AE=
,求出AE=![]() ,
,
当E在直线AD左侧时,先利用勾股定理求出PA=![]() ,PO=
,PO=![]() ,进而得出PE=
,进而得出PE=![]() ,再判断出
,再判断出![]() ,即可得出点E坐标,当E'在直线DA右侧时,即可得出结论.
,即可得出点E坐标,当E'在直线DA右侧时,即可得出结论.
(1)∵点A(1,0),B(0,1)在二次函数y1=kx2+m(k<0)的图象上,
∴![]() ,
,
∴![]() ,
,
∴二次函数解析式为y1=-x2+1,
∵点A(1,0),D(0,-3)在二次函数y2=ax2+b(a>0)的图象上,
∴![]() ,
,
∴![]() ,
,
∴二次函数y2=3x2-3;
(2)设M(m,-m2+1)为第一象限内的图形ABCD上一点,M'(m,3m2-3)为第四象限的图形上一点,
∴MM'=(1-m2)-(3m2-3)=4-4m2,
由抛物线的对称性知,若有内接正方形,
∴2m=4-4m2,
∴m=![]() 或m=
或m=![]() (舍),
(舍),
∵0<![]() <1,
<1,
∴存在内接正方形,此时其边长为![]() ;
;
(3)在Rt△AOD中,OA=1,OD=3,
∴AD=![]() ,
,
同理:CD=![]() ,
,
在Rt△BOC中,OB=OC=1,
∴BC=![]() ,
,
①如图1,当△DBC∽△DAE时,
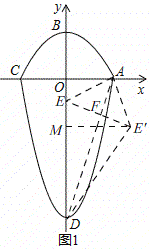
∵∠CDB=∠ADO,
∴在y轴上存在E,由![]() ,
,
∴![]() ,
,
∴DE=![]() ,
,
∵D(0,-3),
∴E(0,-![]() ),
),
由对称性知,在直线DA右侧还存在一点E'使得△DBC∽△DAE',
连接EE'交DA于F点,作E'M⊥OD于M,连接E'D,
∵E,E'关于DA对称,
∴DF垂直平分EE',
∴△DEF∽△DAO,
∴![]() ,
,
∴![]() ,
,
∴DF=![]() ,EF=
,EF=![]() ,
,
∵S△DEE'=![]() DEE'M=EF×DF=
DEE'M=EF×DF=![]() ,
,
∴E'M=![]() ,
,
∵DE'=DE=![]() ,
,
在Rt△DE'M中,DM=![]() ,
,
∴OM=1,
∴E'(![]() ,-1),
,-1),
②如图2,
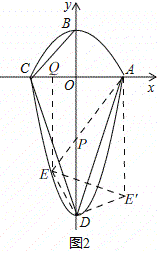
当△DBC∽△ADE时,有∠BDC=∠DAE,![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
当E在直线AD左侧时,设AE交y轴于P,作EQ⊥AC于Q,
∵∠BDC=∠DAE=∠ODA,
∴PD=PA,
设PD=n,
∴PO=3-n,PA=n,
在Rt△AOP中,PA2=OA2+OP2,
∴n2=(3-n)2+1,
∴n=![]() ,
,
∴PA=![]() ,PO=
,PO=![]() ,
,
∵AE=![]() ,
,
∴PE=![]() ,
,
在AEQ中,OP∥EQ,
∴![]() ,
,
∴OQ=![]() ,
,
∵![]() ,
,
∴QE=2,
∴E(-![]() ,-2),
,-2),
当E'在直线DA右侧时,
根据勾股定理得,AE=![]() ,
,
∴AE'=![]()
∵∠DAE'=∠BDC,∠BDC=∠BDA,
∴∠BDA=∠DAE',
∴AE'∥OD,
∴E'(1,-![]() ),
),
综上,使得△BDC与△ADE相似(其中点C与E是对应顶点)的点E的坐标有4个,
即:(0,-![]() )或(
)或(![]() ,-1)或(1,-
,-1)或(1,-![]() )或(-
)或(-![]() ,-2).
,-2).


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
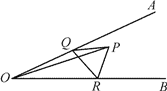
A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面材料:如果![]() (
(![]() )的b次幂等于N,即有指数式
)的b次幂等于N,即有指数式![]() ,那么数b叫做以
,那么数b叫做以![]() 为底N的对数,
为底N的对数,
记作:对数式: ![]()
例如:
(1)因为指数式![]() ,所以以2为底,4的对数是2,对数式记作:
,所以以2为底,4的对数是2,对数式记作:![]()
(2)因为指数式![]() ,所以以4为底,16的对数是2,对数式记作:
,所以以4为底,16的对数是2,对数式记作:![]()
1. 请根据上面阅读材料将下列指数式改为对数试:(1)![]() ;(2)
;(2)![]()
2. 将下列对数式改为指数式:(1)![]() ;(2)
;(2)![]()
3.计算 :![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
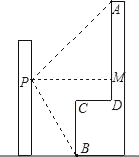
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
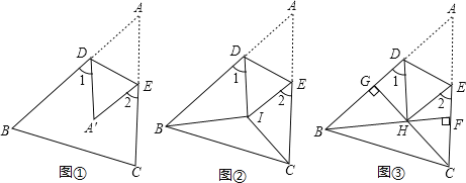
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com