
����Ŀ�����֣�1����ͼ1���ѡ�ABC��DE�۵���ʹ��A���ڵ�A�����������жϡ�1+��2���A�к�������ϵ��ֱ��д����Ľ��ۣ�����˵������
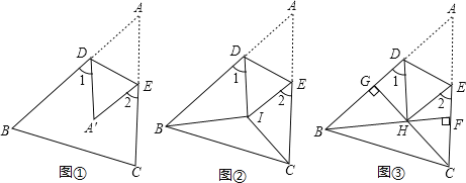
˼����2����ͼ2��BIƽ�֡�ABC��CIƽ�֡�ACB���ѡ�ABC�۵���ʹ��A���I�غϣ�����1+��2=100�㣬���BIC�Ķ�����
��չ��3����ͼ3������ǡ�ABC�У�BF��AC�ڵ�F��CG��AB�ڵ�G��BF��CG���ڵ�H���ѡ�ABC�۵�ʹ��A�͵�H�غϣ���̽����BHC���1+��2�Ĺ�ϵ����֤����Ľ��ۣ�
���𰸡���1����1+��2=2��A�����ɼ���������2����BIC=115�㣻��3����BHC=180��-![]() ����1+��2����
����1+��2����
��������
��1�����ݷ��۱任�����ʡ��������ڽǺͶ������Լ�ƽ�ǵĶ���������ɣ�
��2�����������ν�ƽ���ߵ����ʵó���IBC+��ICB=90��-![]() ��A�����������ε��ڽǺͶ������������BIC�Ķ����ɣ�
��A�����������ε��ڽǺͶ������������BIC�Ķ����ɣ�
��3�����ݴ��ߵ����ʵó�����AFH+��AGH=90��+90��=180�����������ı���AGHF���ڽǺ�Ϊ360�㣬��ʾ��![]() ��
��![]() �Ĺ�ϵ�����öԶ��ǵ����������õ�
�Ĺ�ϵ�����öԶ��ǵ����������õ�![]() ��
��![]() �Ĺ�ϵ���ٽ�ϵڣ�1���ʣ��õ���BHC���1+��2�Ĺ�ϵ��
�Ĺ�ϵ���ٽ�ϵڣ�1���ʣ��õ���BHC���1+��2�Ĺ�ϵ��
�⣺��1����1+��2=2��A��
���ɣ����ݷ��۵����ʣ���ADE=![]() ��180��-��1������AED=
��180��-��1������AED=![]() ��180��-��2����
��180��-��2����
�ߡ�A+��ADE+��AED=180�㣬
���A+![]() ��180-��1��+
��180-��1��+![]() ��180-��2��=180�㣬
��180-��2��=180�㣬
������2��A=��1+��2��
��2��![]() �ɣ�1��֪����1+��2=2��A��
�ɣ�1��֪����1+��2=2��A��
��![]() ��1+��2=100�㣬
��1+��2=100�㣬
���A=50��
��IBƽ�֡�ABC��ICƽ�֡�ACB��
���IBC+��ICB=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=90��-
��180��-��A��=90��-![]() ��A��
��A��
���BIC=180��-����IBC+��ICB��=180��-��90��-![]() ��A��=90��+
��A��=90��+![]() ��A=90��+
��A=90��+![]() ��50��=115�㣻
��50��=115�㣻
��3����BF��AC��CG��AB��
���AFH+��AGH=90��+90��=180�㣬
���FHG+��A=180�㣬
���BHC=��FHG=180��-��A��
�ɣ�1��֪��1+��2=2��A��
���A=![]() ����1+��2����
����1+��2����
���BHC=180��-![]() ����1+��2����
����1+��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ͼ��ABCD�����������κ���y1=kx2+m��k��0����y2=ax2+b��a��0���IJ���ͼ��Χ�ɵķ��ͼ�Σ���֪A��1��0����B��0��1����D��0����3����
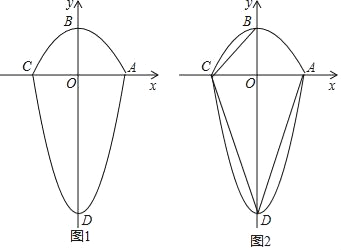
��1��ֱ��д�����������κ����ı���ʽ��
��2���ж�ͼ��ABCD�Ƿ�����ڽ������Σ������ε��ĸ�������ͼ��ABCD�ϣ�����˵�����ɣ�
��3����ͼ2������BC��CD��AD��������ƽ���ڣ���ʹ����BDC����ADE���ƣ����е�C���E�Ƕ�Ӧ���㣩�ĵ�E������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������1�������ϵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ʾ��0�� 2 ��3��5�� 4 ������������⣮
�ֱ��ʾ��0�� 2 ��3��5�� 4 ������������⣮
�ٻ��������ʾ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]()
��![]() ��
��![]() ����֮��ľ����� ��
����֮��ľ����� ��
��![]() ��
��![]() ����֮��ľ����� ��
����֮��ľ����� ��
��![]() ��
�� ![]() ����֮��ľ����� ��
����֮��ľ����� ��
��2����˼��������![]() ��ʾ��
��ʾ��![]() ��
��![]() ����
���� ![]() ��ʾ��
��ʾ��![]() ����
���� ![]() �����ú�
�����ú� ![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ ![]() ��
��![]() ���� ��ľ����� ��
���� ��ľ����� ��
��3������ɣ�����![]() ��ʾ��
��ʾ��![]() ����
���� ![]() ��ʾ��
��ʾ��![]() ����
���� ![]() ��
��![]() �����ľ����ú�
�����ľ����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ�� ��
�Ĵ���ʽ��ʾ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��OE��AB��BC�ڵ�E.��AD��8cm����OE�ij�Ϊ�� ��
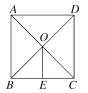
A. 3cm B. 4cm C. 6cm D. 8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���(m��1)x2��x��2��0.
(1)��x����1�Ƿ��̵�һ��������m��ֵ�ͷ��̵���һ����
(2)��mΪ��ʵ��ʱ����������������ȵ�ʵ������
(3)��x1��x2�Ƿ��̵�����ʵ��������xx2��x1x����![]() ������ʵ��m��ֵ��
������ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABE�У���BAE��105�㣬AE�Ĵ�ֱƽ����MN��BE�ڵ�C����AB��CE������B�Ķ�����(����)

A. 45��B. 60��C. 50��D. 55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��������������ֱ�ΪA����1����2����B����1����4����C��2����3����
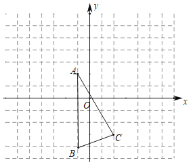
��1������ABC������ƽ��4����λ��������ƽ��6����λ���õ���A1B1C1��������A1B1C1���߶�AC��ƽ�ƹ�����ɨ�����Ϊ�� ����
��2��������A1B1C1����y��ԳƵ�ͼ�Ρ�A2B2C2��������C2Ϊ�� ����
��3������ABD���ABCȫ�ȣ����D������Ϊ�� ������C���D���غϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
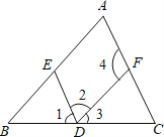
����Ŀ������ͼ����������������̣�
��1���ߡ�2+��4=180����
��DE��AC ��______����
��2���ߡ�1=��C��
��DE��______��______����
��3����AB��DF��
���2=��______��______����
��4����______��______��
���B=��3 ��______����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
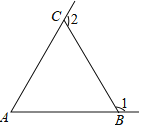
����Ŀ����ͼ����ABC�У�AC=BC��AB.����1����2�ֱ�Ϊ��ABC����ACB����ǣ������нǶȹ�ϵ������ȷ�� ��
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com