
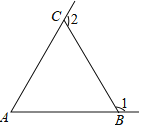
【题目】如图,△ABC中,AC=BC<AB.若∠1、∠2分别为∠ABC、∠ACB的外角,则下列角度关系何者正确( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】
首先我们要清楚,长边对大角,即越长的边所对的角越大,等边对等角,即相等的边对应的角相等.选项中判断∠1与∠2的关系和∠A+∠2,∠A+∠1与180°的关系,都可以可以通过三角形的一个外角等于与它不相邻的两个内角和等量代换去判断.
由三角形的一个外角等于与它不相邻的两个内角和可知:
∠1=∠A+∠ACB,∠2=∠A+∠ABC
而∠ACB与∠ABC所对的边是AB和AC,AB >AC
所以∠ACB>∠ABC
所以∠1>∠2,故排除选项A,B
又∠A+∠2=∠A+∠A+∠ABC,∠A+∠1=∠A+∠A+∠ACB,∠ACB +∠A+∠ABC=180°
因为∠A与∠ACB所对的边是BC和AB,BC<AB
∠A与∠ABC所对的边是BC和AC,BC=AC
所以∠A<∠ACB,∠A=∠ABC
所以∠A+∠A+∠ABC<∠ACB +∠A+∠ABC,∠A+∠A+∠ACB=∠ACB +∠A+∠ABC
即∠A+∠2<180°,∠A+∠1=180°
故选项C正确,D选项排除.
故答案为C


科目:初中数学 来源: 题型:
【题目】发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
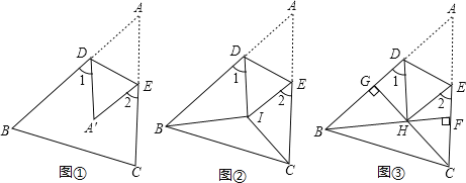
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程![]()
(1)求证:方程总有两个不相等的实数根。
(2)m为何整数时,此方程的两个根都是正整数?
(3)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
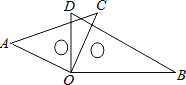
【题目】如图,将一副三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=()度。
A. 小于180 B. 大于180 C. 等于180 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
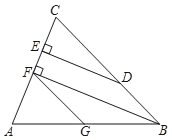
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个,黄球1个,从中任意摸出1球是黄球的概率是![]() .
.
(1)试求口袋中绿球的个数;
(2)小明第一次从口袋中任意摸出1球,不放回搅匀,第二次再摸出1球.请用列表或画树状图的方法求摸出“一绿一黄”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com