
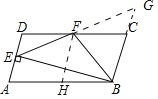
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
如图延长EF交BC的延长线于G,取AB的中点H连接FH.证明△DFE≌△FCG 得EF=FG,BE⊥BG,四边形BCFH是菱形即可解决问题;
如图延长EF交BC的延长线于G,取AB的中点H连接FH.
∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△FCG,
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确,
故选:D.


科目:初中数学 来源: 题型:
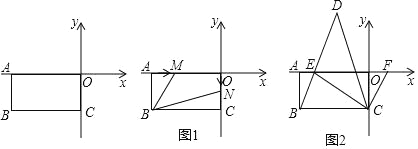
【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+![]() =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写大赛”,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:

请根据所给信息,解答下列各题:
(1)a= ;
(2)请把频数分布直方图补充完整;
(3)若测试成绩在90分以上(包括90分)为“优”等,则该校参加这次比赛的3 000名学生中成绩为“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: .
.
请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.
![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
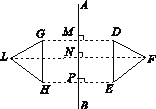
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点______________;
(2)分别延长DM,EP,FN至点____________,使______=______,______=______,______=______;
(3)顺次连结______,______,______,就得到△DEF关于直线AB的对称图形△GHL.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com