
【题目】如图所示,已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
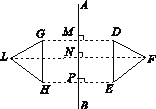
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点______________;
(2)分别延长DM,EP,FN至点____________,使______=______,______=______,______=______;
(3)顺次连结______,______,______,就得到△DEF关于直线AB的对称图形△GHL.
【答案】(1)M,P,N;(2)G,H,L,MG,DM ,PH,EP,NL,FN;(3)GH,HL,LG
【解析】
作轴对称图形就是从图形的各顶点向轴引垂线并延长相同长度找对应点,顺次连接所成的图形.根据这个作法对(1)、(2)、(3)进行求解即可.
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点M、P、N;
(2)分别延长DM,EP,FN至点G、H、L,使MG=DM, PH=EP, NL=FN;
(3)顺次连结GH,HL,LG,就得到△DEF关于直线AB的对称图形△GHL.
故答案为:(1)M,P,N;
(2)G,H,L,MG,DM, PH,EP, NL,FN;
(3)GH,HL,LG.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】向日葵水果店推出甲乙两种礼盒,甲礼盒中有樱桃![]() 千克,枇杷
千克,枇杷![]() 千克,香梨
千克,香梨![]() 千克,乙礼盒中有樱桃
千克,乙礼盒中有樱桃![]() 千克,枇杷
千克,枇杷![]() 千克,哈蜜瓜
千克,哈蜜瓜![]() 千克,己知樱桃每千克
千克,己知樱桃每千克![]() 元,甲礼盒每盒
元,甲礼盒每盒![]() 元,乙礼盒每盒
元,乙礼盒每盒![]() 元,当然,顾客也可根据需要自由搭配,小陶用
元,当然,顾客也可根据需要自由搭配,小陶用![]() 元买乙礼盒和自由搭配礼盒(香梨
元买乙礼盒和自由搭配礼盒(香梨![]() 千克,枇杷
千克,枇杷![]() 千克,哈蜜瓜
千克,哈蜜瓜![]() 千克)若干盒,则小陶一共可买礼盒____个.
千克)若干盒,则小陶一共可买礼盒____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A, ![]() .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 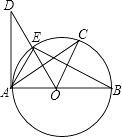
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,按如下步骤作图: ①分别以点B、C为圆心,大于 ![]() AB的长为半径作弧,两弧相交于点M和N;
AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 . 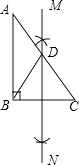
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).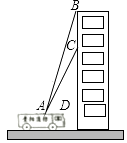
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 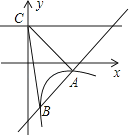
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com