
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 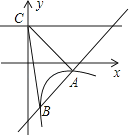
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
【答案】
(1)
解:把A(2,﹣1)代入反比例解析式得:﹣1= ![]() ,即m=﹣2,
,即m=﹣2,
∴反比例解析式为y=﹣ ![]() ,
,
把B( ![]() ,n)代入反比例解析式得:n=﹣4,即B(
,n)代入反比例解析式得:n=﹣4,即B( ![]() ,﹣4),
,﹣4),
把A与B坐标代入y=kx+b中得: 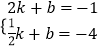 ,
,
解得:k=2,b=﹣5,
则一次函数解析式为y=2x﹣5.
(2)
解:∵A(2,﹣1),B( ![]() ,﹣4),直线AB解析式为y=2x﹣5,
,﹣4),直线AB解析式为y=2x﹣5,
∴AB= ![]() =
= ![]() ,原点(0,0)到直线y=2x﹣5的距离d=
,原点(0,0)到直线y=2x﹣5的距离d= ![]() =
= ![]() ,
,
则S△ABC= ![]() ABd=
ABd= ![]() .
.
【解析】(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)利用两点间的距离公式求出AB的长,利用点到直线的距离公式求出点C到直线AB的距离,即可确定出三角形ABC面积.此题考查了反比例函数与一次函数的交点问题,熟练掌握待定系数法是解本题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
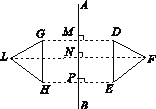
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点______________;
(2)分别延长DM,EP,FN至点____________,使______=______,______=______,______=______;
(3)顺次连结______,______,______,就得到△DEF关于直线AB的对称图形△GHL.
查看答案和解析>>
科目:初中数学 来源: 题型:
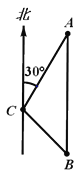
【题目】如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C处80海里,轮船沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到达航线AB的距离;
(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ADC=∠EFC,∠3=∠C,证明∠1=∠2的过程如下,请填上对应的理由.
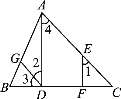
解:∵∠ADC=∠EFC(已知),
∴AD∥EF(___________________________________).
∴∠1=∠4(__________________________________).
又∵∠3=∠C(已知),
∴AC∥DG(__________________________________).
∴∠2=∠4(_________________________________).
∴∠1=∠2(________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点.如果以点
轴上的点.如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则![]() 的坐标为__________.
的坐标为__________.
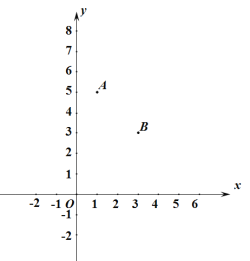
查看答案和解析>>
科目:初中数学 来源: 题型:
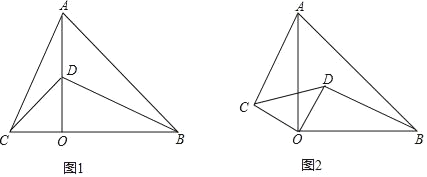
【题目】已知,△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,连接AC,BD.
(1)如果△AOB,△COD的位置如图1所示,点D在AO上,请判断AC与BD的数量关系,并说明理由;
(2)如果△AOB,△COD的位置如图2所示,请判断AC与BD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.

A.14B.15C.16D.17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com