
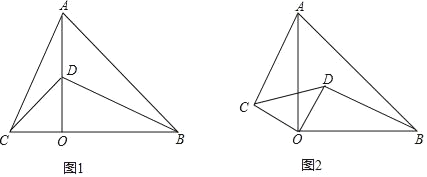
【题目】已知,△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,连接AC,BD.
(1)如果△AOB,△COD的位置如图1所示,点D在AO上,请判断AC与BD的数量关系,并说明理由;
(2)如果△AOB,△COD的位置如图2所示,请判断AC与BD的数量关系,并说明理由.
【答案】(1)结论:AC=BD.理由见解析;(2)(1)结论:AC=BD.理由见解析.
【解析】
(1)利用SAS证明△AOC≌△BOD,根据全等三角形的性质即可得;
(2)先证明∠AOC=∠BOD,继而根据SAS证明△AOC≌△BOD,即可解决问题.
(1)结论:AC=BD.
理由:∵△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OC=OD,
在△AOC和△BOD中,
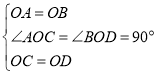 ,
,
∴△AOC≌△BOD,
∴AC=BD;
(2)结论:AC=BD.
理由:∵△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OC=OD,∠AOC=∠BOD,
在△AOC和△BOD中,
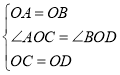 ,
,
∴△AOC≌△BOD,
∴AC=BD.


科目:初中数学 来源: 题型:
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).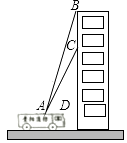
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 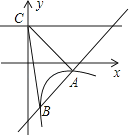
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△MCD平移至△NBA.
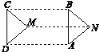
(1)图中平行且相等的线段有____________;
(2)图中相等的角有_______________ (写出三对即可);
(3)能够完全重合的三角形是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
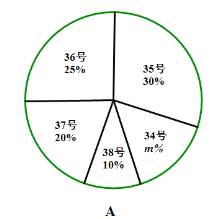
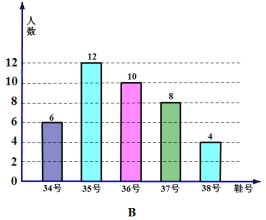
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光![]() ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
(1)本次随机抽样的学生数是多少?A中![]() 值是多少?
值是多少?
(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.

解法展示:证明:延长BE交直线CD于点M,如图所示.

∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5 cm或6.5 cm
B.2.5 cm
C.6.5 cm
D.5 cm或13cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com