
����Ŀ��һ��������ij����ʻ�����У������е�ʣ������y����������ʻ·��x��ǧ�ף�֮����һ�κ�����ϵ���䲿��ͼ����ͼ��ʾ��
��1����y����x�ĺ�����ϵʽ��������Ҫд������
��2����֪�������е�ʣ������Ϊ8��ʱ���������Ὺʼ��ʾ���ͣ��ڴ˴���ʻ�����У���ʻ��500ǧ��ʱ��˾��������ǰ������ļ���վ��30ǧ��·�̣��ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·���Ƕ���ǧ�ף�

���𰸡���1����һ�κ�������ʽΪy=��![]() x+60����2���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�
x+60����2���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�
��������
��1�����ݺ���ͼ���е���������ô���ϵ�������һ�κ�������ʽ��
��2������һ�κ���ͼ���ϵ�����������������ʣ������Ϊ8��ʱ��ʻ��·�̣�������ô�.
��1�����һ�κ�������ʽΪy=kx+b��
����150��45������0��60������y=kx+b����
![]() ����ã�
����ã�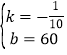 ��
��
���һ�κ�������ʽΪy=��![]() x+60��
x+60��
��2����y=��![]() x+60=8ʱ��
x+60=8ʱ��
���x=520��
����ʻ520ǧ��ʱ�������е�ʣ������Ϊ8����
530��520=10ǧ�ף�
�����е�ʣ������Ϊ8��ʱ���������վ10ǧ����
���ڿ����ü���վ��;�У�������ʼ��ʾ���ͣ���ʱ�����վ��·����10ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AOB�У���AOB=90�㣬�Ե�AΪԲ�ģ�OA�ij�Ϊ�뾶�� ![]() ��
�� ![]() �ڵ�C����OA=2������Ӱ���ֵ����Ϊ ��
�ڵ�C����OA=2������Ӱ���ֵ����Ϊ �� 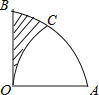
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������y= ![]() ��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH=
��k��0����ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH=3��tan��AOH= ![]() ����B������Ϊ��m����2����
����B��������m����2���� 
��1�����AHO���ܳ���
��2����÷�����������һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ADC����EFC����3����C��֤����1����2�Ĺ������£������϶�Ӧ������.
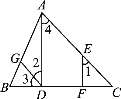
�⣺�ߡ�ADC����EFC����֪����
��AD��EF��___________________________________����
���1����4��__________________________________����
�֡ߡ�3����C����֪����
��AC��DG��__________________________________����
���2����4��_________________________________����
���1����2��________________________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ���ϵĵ㣮����Ե�
���ϵĵ㣮����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ���
Ϊ������ı�����ƽ���ı��Σ���![]() ������Ϊ__________��
������Ϊ__________��
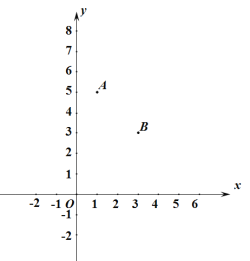
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У���A��52��������ABC���ACB�Ľ�ƽ���߽��ڵ�D1���õ���D1����ABD1���ACD1�Ľ�ƽ���߽��ڵ�D2���õ���D2���������ƣ���ABD4���ACD4�Ľ�ƽ���߽��ڵ�D5���õ���D5�����D5�Ķ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
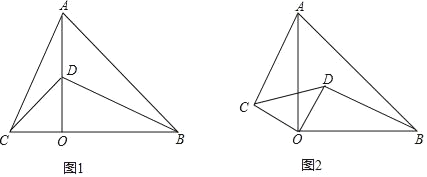
����Ŀ����֪����AOB����COD���й����������������ֱ�������Σ���AOB����COD��90��������AC��BD��
��1�������AOB����COD��λ����ͼ1��ʾ����D��AO�ϣ����ж�AC��BD��������ϵ����˵�����ɣ�
��2�������AOB����COD��λ����ͼ2��ʾ�����ж�AC��BD��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210�������ÿ����Ʒ���ۼ�ÿ����lԪ����ÿ��������l0��(ÿ���ۼ۲��ܸ���65Ԫ)����ÿ����Ʒ���ۼ���xԪ(xΪ������)��ÿ���µ���������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��ֱ��д���Ա������ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ���������?�����������Ƕ���Ԫ?
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���µ�����ǡΪ2200Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪�ȱ�������ABC�͵ȱ�������DBC�й�����BC����ͼ��ij����Ϊ��ת���ģ���ת��DBCʹ������ABC�غϣ�����ת���Ŀ�����________��(д��һ����ת���ļ���)

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com