练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，已知等边三角形ABC和等边三角形DBC有公共边BC，以图中某个点为旋转中心，旋转△DBC使它和△ABC重合，则旋转中心可以是________．(写出一个旋转中心即可)

    【答案】点B(或点C或BC的中点)

    【解析】

    首先由等边三角形的性质可得多条相等的边和多个相等的角，此时结合旋转的定义即可判断点B和点C是否满足题意，接下来在考虑BC的中点是否满足题意，据此进行解答即可。

    根据△DBC和△ABC都是等边三角形求有公共边BC，因此AB=BC=AC=DB=DC， ,所以将△DBC绕着B点逆时针旋转 或绕着C点旋转，都能和△ABC重合；将△DBC绕着BC的中点旋转 也能和△ABC重合，故满足条件的点有B、C、BC的中点。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

    （1）求y关于x的函数关系式；（不需要写定义域）

    （2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图，已知AB∥CD，∠1=∠2，求证：∠3=∠4.

    解法展示：证明：延长BE交直线CD于点M，如图所示.

    ∵AB∥CD，∴∠1=∠BMC（根据1）.

    ∵∠1=∠2，∴∠2=∠BMC（根据2）.

    ∴BE∥CF（根据3）.

    ∴∠3=∠4（根据4）.

    反思交流：（1）解法展示中的根据1是______________，根据2是______________，根据3是_____________，根据4是____________.

    （2）上述命题中，条件记为：①AB∥CD，②∠1=∠2，结论记为：③∠3=∠4.若把其中的一个条件和结论对调，得到一个新命题，写出这个命题（用序号表示即可），判断新命题的真假，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展开后，得折痕AD、BE．(如图①)，点O为其交点．如图②，若P、N分别为BE、BC上的动点．如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值=_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据要求，解答下列问题．

    （1）解方程组： ．

    （2）解下列方程组，只写出最后结果即可：①；②．

    （3）以上每个方程组的解中，x值与y值有怎样的大小关系？

    （4）观察以上每个方程组的外形特征，请你构造一个具有此特征的方程组，并用（3）中的结论快速求出其解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC于F，若AF=6，则四边形AEDF的周长是（　 　）

    A. 24 B. 28 C. 32 D. 36

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个点到圆的最小距离为4cm，最大距离为9cm，则该圆的半径是（　　）
    A.2.5 cm或6.5 cm
    B.2.5 cm
    C.6.5 cm
    D.5 cm或13cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

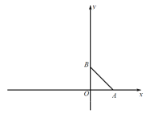
    【题目】平面直角坐标系中，点A、B分别在x轴正半轴、y轴正半轴上，AO=BO，△ABO的面积为8.

    （1）求点A的坐标；

    （2）点C、D分别在x轴负半轴、y轴正半轴上（D在B点上方），AB⊥CD于E，设点D纵坐标为t，△BCE的面积为S，求S与t的函数关系；

    （3）在（2）的条件下，点F为BE中点，连接OF交BC于G，当∠FOB+∠DAE=45°时，求点E坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．

    （1）经过多长时间，四边形PQCD是平行四边形？

    （2）经过多长时间，四边形PQBA是矩形？

    （3）经过多长时间，当PQ不平行于CD时，有PQ=CD．

    查看答案和解析>>

    同步练习册答案