
【题目】根据要求,解答下列问题.
(1)解方程组:![]() .
.
(2)解下列方程组,只写出最后结果即可:①![]() ;②
;②![]() .
.
(3)以上每个方程组的解中,x值与y值有怎样的大小关系?
(4)观察以上每个方程组的外形特征,请你构造一个具有此特征的方程组,并用(3)中的结论快速求出其解.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)x=y;(4)见解析.
;(3)x=y;(4)见解析.
【解析】
(1)方程组利用加减消元法求出解即可;
(2)分别求出两个方程组的解即可;
(3)观察得到x与y的关系即可;
(4)写出满足此特征的方程组,把x=y代入任何一个方程求出解即可.
解:(1)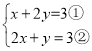 ,
,
①×2﹣②得:3y=3,即y=1,
把y=1代入①得:x=1,
则方程组的解为 ![]() ;
;
(2)① ,
,
①×3得:9x+6y=30 ③,
②×2得:4x+6y=20 ④,
由③-④得:5x=10,x=2,
把x=2代入①得:y=2,
∴![]() ;
;
② ,
,
①×2得:4x-2y=8 ③,
③+②得:3x=12,x=4,
把x=2代入①得:y=4,
∴![]() ;
;
(3)以上每个方程组的解中,x=y;
(4)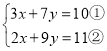
把x=y代入①得:3y+7y=10,即y=1,
则方程组的解为![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点.如果以点
轴上的点.如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则![]() 的坐标为__________.
的坐标为__________.
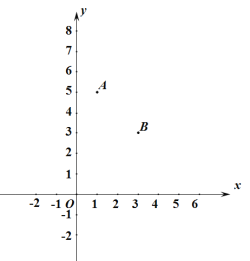
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
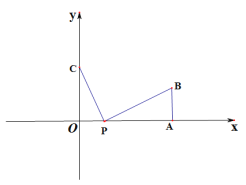
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.

A.14B.15C.16D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知等边三角形ABC和等边三角形DBC有公共边BC,以图中某个点为旋转中心,旋转△DBC使它和△ABC重合,则旋转中心可以是________.(写出一个旋转中心即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() . 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
. 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com