
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
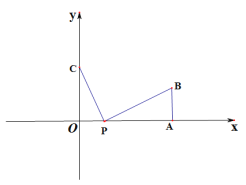
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
【答案】(1)![]() 的值为
的值为![]() ;(2)当
;(2)当![]() 最小时,t的值为15;(3)
最小时,t的值为15;(3)![]() .
.
【解析】
(1)先根据二次根式的被开方数的非负性求出a、b的值,从而可得OA、OC的长,再利用勾股定理分别求出PB、PC的长,从而可得出答案;
(2)如图(见解析),作点B关于x轴的对称点![]() ,从而可得
,从而可得![]() 的长,再根据两点之间线段最短确认
的长,再根据两点之间线段最短确认![]() 最小时点P的位置,然后根据等腰直角三角形的性质求解即可得;
最小时点P的位置,然后根据等腰直角三角形的性质求解即可得;
(3)先根据题(1)得出![]() 的式子,可发现与所求的
的式子,可发现与所求的![]() 的形式完全一样,因此,参照题(2)的方法,画出图形,利用几何方法求解即可(与题(2)的思路完全相同).
的形式完全一样,因此,参照题(2)的方法,画出图形,利用几何方法求解即可(与题(2)的思路完全相同).
![]()
![]() ,解得
,解得![]()
将![]() 代入得,
代入得,![]()
![]()
![]()
(1)当![]() 时,则
时,则![]()
![]() 轴
轴
![]()
![]()
![]()
故![]() 的值为
的值为![]() ;
;
(2)如图1,作点B关于x轴的对称点![]() ,过点
,过点![]() 作
作![]() 轴于点D,连接
轴于点D,连接![]() ,
,![]() 交x轴于点
交x轴于点![]()
由轴对称的性质得:![]()
![]()
由两点之间线段最短得:当点P与点![]() 重合时,
重合时,![]() 最小,最小值为
最小,最小值为![]()
![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]()
故当![]() 最小时,t的值为15;
最小时,t的值为15;
(3)由(1)知,![]()
因此,对于![]() 可参照(2)的方法,画出如图2,其中,点B与点
可参照(2)的方法,画出如图2,其中,点B与点![]() 关于x轴对称,
关于x轴对称,![]() 轴,
轴,![]()
则![]()
由(2)可知,![]() 的最小值为
的最小值为![]()
![]()
![]()
即![]() 的最小值为
的最小值为![]()
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2. 
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
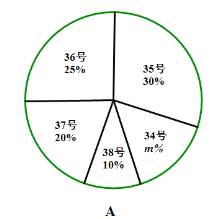
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光![]() ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
(1)本次随机抽样的学生数是多少?A中![]() 值是多少?
值是多少?
(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
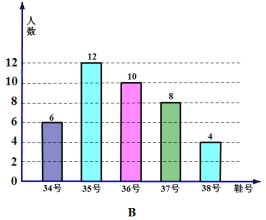
查看答案和解析>>
科目:初中数学 来源: 题型:
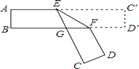
【题目】把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.

解法展示:证明:延长BE交直线CD于点M,如图所示.

∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 ![]() 的长为 .
的长为 . 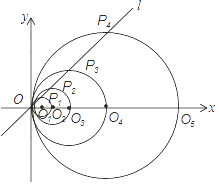
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题.
(1)解方程组:![]() .
.
(2)解下列方程组,只写出最后结果即可:①![]() ;②
;②![]() .
.
(3)以上每个方程组的解中,x值与y值有怎样的大小关系?
(4)观察以上每个方程组的外形特征,请你构造一个具有此特征的方程组,并用(3)中的结论快速求出其解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.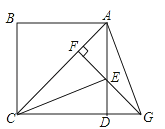
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com